 |
|
Differenzialrechnung | Begriffe und Themengebiete |
|

Differenzialrechnung - Begriffserläuterung
| Die Differenzialrechnung ist ein wesentlicher Bestandteil der Analysis. Sie ist eng verwandt mit der Integralrechnung, mit der sie unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird. Zentrales Thema der Differenzialrechnung ist die Berechnung lokaler Veränderungen von Funktionen. | |
|
|
| In vielen Fällen ist die Differenzialrechnung ein unverzichtbares Hilfsmittel zur Bildung mathematischer Modelle, die versuchen, die Wirklichkeit abzubilden, sowie zu deren nachfolgender Analyse. Die Entsprechung der Ableitung im untersuchten Sachverhalt ist häufig die momentane (auch lokale) Änderungsrate. In den Wirtschaftswissenschaften spricht man auch häufig von Grenzraten (z.B. Grenzkosten, Grenzproduktivität eines Produktionsfaktors etc.). | |
| Der Grundbegriff der Differenzialrechnung ist die Ableitung einer Funktion. In geometrischer Sprache ist die Ableitung eine verallgemeinerte Steigung. Der geometrische Begriff Steigung ist ursprünglich nur für lineare Funktionen definiert, deren Funktionsgraph eine Gerade ist. Die Ableitung einer beliebigen Funktion an einer Stelle x0 definiert man als die Steigung der Tangenten im Punkt (x0|f(x0) des Graphen von f. In arithmetischer Sprache gibt die Ableitung einer Funktion f für jedes x an, wie groß der lineare Anteil der Änderung von f(x) ist (die Änderung 1. Ordnung), wenn sich x um einen beliebig kleinen Betrag Δx ändert. Für die exakte Formulierung dieses Sachverhalts wird der Begriff Grenzwert (oder limes) verwendet. In einer klassischen physikalischen Anwendung liefert die Ableitung der Orts- oder Weg-Zeit-Funktion nach der Zeit die Momentangeschwindigkeit eines Teilchens. |
|
| Quelle: WIKIPEDIA Differenzialrechnung |
Begriffe und Themengebiete
| In diesem Teil des Portals lernen und üben wir, wie man den graphischen Verlauf einer Funktionsgleichung und deren Funktionsverhalten mit mathematischen Mitteln bestimmen kann. Hierzu stehen uns die unterschiedlichsten Werkzeuge und Regeln zur Verfügung, wie aus nachfolgender Grafik ersichtlich ist. |
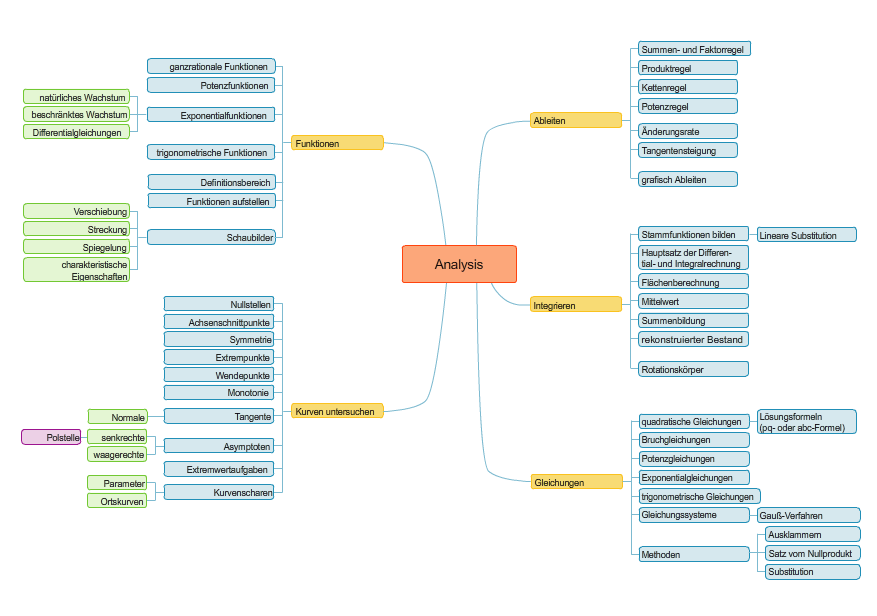 |
| Das Thema „Integrieren“ ist Gegenstand des Menüpunktes „Integralrechnung“. Im ersten Untermenü „Änderungsraten“ lernen wir, wie aus der Steigung durch zwei Punkte des Graphen einer Funktion (genannt mittlere Änderungsrate) die Steigung der Kurve in einem bestimmten Punkt (genannt momentane oder lokale Änderungsrate) hergeleitet wird. Das Untermenü „Ableitungen“ bringt uns dann die Rechenregeln für die schnelle Berechnung der Tangentensteigung einer Kurve in einem beliebigen Punkt derselben näher. Das Untermenü „Graphen und Funktionen analysieren“ beschäftigt sich unabhängig von der jeweiligen Funktionsklasse mit dem Thema „Kurven untersuchen“. Wir lernen wie wir charakteristische Punkte des Graphen einer Funktion bestimmen, was sich hinter "globalem Verhalten", „Monotonie- und Krümmungsverhalten“ verbirgt, was "Punktsymmetrie" bzw. "Achsensymmetrie" bedeutet, wie wir „Asymptoten und Pole“ bestimmen und letztendlich "Achsenschnittpunkte", "Extremstellen" sowie „Wendestellen“ analysieren. Das Untermenü „Funktionsklassen“ beschäftigt sich mit den rechnerischen Themen „Kurven untersuchen“ des zuvor benannten Untermenüs. Wir berechnen „Nullstellen“, „Achsenschnittpunkte“, „Extrempunkte“, „Wendepunkte“, „Monotonie- und Krümmungsverhalten“, „Tangenten und Normale“ gefolgt von „Globalem Verhalten“, „Symmetrie“, „Asymptoten und Pole“ sowie „Kurvenscharen“, und dies für jeden einzelnen Funktionstyp (siehe Kasten „Funktionen“ in obiger Grafik). Im Untermenü „Grafisches Differenzieren und Integrieren“ lernen wir die Abhängigkeit von Extremstellen, Wendestellen, Nullstellen sowie dem Monotonie- und Krümmungsverhalten der Graphen der Ausgangsfunktion und deren ersten, zweiten und dritten Ableitung kennen und wie wir dies an den Graphen von Funktionen, deren Funktionsgleichung nicht bekannt ist, erkennen. |
| Für Absolventen der beruflichen und technischen Gymnasien sieht die Grafik geringfügig anders aus. |
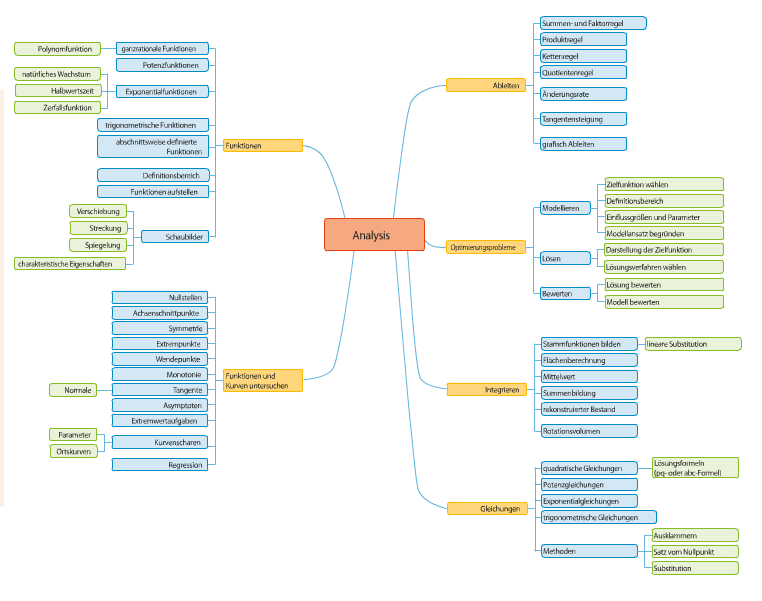 |
| Hier finden wir das zusätzliche Thema „Optimierungsprobleme“ mit den Unterthemen „Modellieren“, „Lösen“ und „Bewerten“. Dieses Thema wird speziell im Untermenüpunkt „Optimieren und Modellieren“ behandelt. Erwähnt werden muss, dass Teilgebiete dieses Themas auch in den allgemeinbildenden Gymnasien behandelt werden. |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 23. November 2021 23. November 2021



