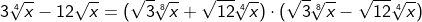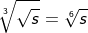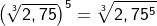|
WIKI zur Wurzelrechnung und den Wurzelgesetzen allgemein |

1. Einführung in das Wurzelziehen
| In der Mathematik versteht man unter Wurzelziehen oder Radizieren die Bestimmung der Unbekannten x in der Potenz | |
| a=xn | |
| Hierbei ist n eine natürliche Zahl größer als 1 und a eine nichtnegative reelle Zahl. Das Ergebnis des Wurzelziehens bezeichnet man als Wurzel oder Radix (von lat. radix „Wurzel“). Das Radizieren ist eine Umkehrung des Potenzierens. Im Fall n=2 spricht man von Quadratwurzeln, bei n=3 von Kubikwurzeln. | |
| Es sei n>1 eine natürliche Zahl. Ist a eine nichtnegative reelle Zahl, so besitzt die Gleichung xn=a genau eine nichtnegative Lösung. Diese wird als n-te Wurzel aus a bezeichnet. Wir schreiben dafür | |
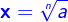 |
|
Hierbei bezeichnet man 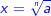 als Wurzel oder Radix, n als Wurzelexponent, a als Radikand oder Wurzelbasis. Üblicherweise wird die zweite Wurzel als Quadratwurzel oder einfach nur als die Wurzel bezeichnet und der Wurzelexponent weggelassen: als Wurzel oder Radix, n als Wurzelexponent, a als Radikand oder Wurzelbasis. Üblicherweise wird die zweite Wurzel als Quadratwurzel oder einfach nur als die Wurzel bezeichnet und der Wurzelexponent weggelassen: |
|
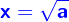 |
|
| Die Wurzeln mit dem Wurzelexponenten 3 (dritte Wurzeln) bezeichnet man auch als Kubikwurzeln. | |
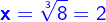 |
|
| (Sprich: Die dritte Wurzel aus 8 ist 2 oder Die Kubikwurzel aus 8 ist 2). | |
Das Operatorsymbol 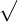 stammt von dem kleinen Buchstaben r ab und steht für radizieren. Er wurde erstmalig 1525 vom deutschen Mathematiker Christoph Rudolff verwendet. Die Verlängerung des r über den vollständigen Term wurde erst später eingeführt. stammt von dem kleinen Buchstaben r ab und steht für radizieren. Er wurde erstmalig 1525 vom deutschen Mathematiker Christoph Rudolff verwendet. Die Verlängerung des r über den vollständigen Term wurde erst später eingeführt. |
 Christoph Rudolff Mathematiker (16. Jahrhundert) |
Merksatz Wurzelziehen
| Wurzelziehen oder Radizieren ist die Umkehrrechenart des Potenzierens, sofern die Basis des Potenzierens die Unbekannte x ist. Der Wert a ist bekannt (z. b. 8) sowie die Potenz n (z. B. 3) zur Basis x und wir suchen den Wert von x. |
Merksatz Wurzelergebnis
Ist der Wurzelexponent n von 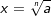 eine gerade Zahl mit a>0, so gibt es zwei Lösungen für x, eine positive und eine negative Lösung. Soll die negative Lösung mitberücksichtigt werden, so muss eine gerade Zahl mit a>0, so gibt es zwei Lösungen für x, eine positive und eine negative Lösung. Soll die negative Lösung mitberücksichtigt werden, so muss 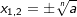 geschrieben werden. geschrieben werden.Lautet eine Aufgabe nur 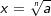 , so wird nur die positive Lösung gesucht. , so wird nur die positive Lösung gesucht. 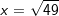 hat die Lösungsmenge L={7}. Lautet die Aufgabenstellung hingegen x2=49, so werden diejenigen positiven und negativen Zahlen gesucht, deren Quadrat 49 ist. Die Lösungsmenge lautet jetzt L={-7;7}. hat die Lösungsmenge L={7}. Lautet die Aufgabenstellung hingegen x2=49, so werden diejenigen positiven und negativen Zahlen gesucht, deren Quadrat 49 ist. Die Lösungsmenge lautet jetzt L={-7;7}. |
Merksatz Wurzelziehen ungerader Exponent
Ist der Wurzelexponent n von 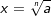 eine ungerade Zahl, so gibt es nur eine Lösungen für x. Die Lösung ist positiv, für a>0 und negativ für a<0. eine ungerade Zahl, so gibt es nur eine Lösungen für x. Die Lösung ist positiv, für a>0 und negativ für a<0.Ist a<0, so muss das Minuszeichen vor die Wurzel geschrieben werden. Die Wurzelregeln besagen, dass negative Werte unter einer Wurzel einen nicht lösbaren Ausdruck darstellen. |
Merksatz Wurzelziehen gerader Exponent
Ist der Wurzelexponent n von 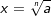 eine gerade Zahl mit a<0, so gibt es keine Lösungen für x, da eine gerade Anzahl von "-"-Multiplikatioinen immer "+" ergibt. Die Lösungsmenge einer solchen Gleichung ist leer. eine gerade Zahl mit a<0, so gibt es keine Lösungen für x, da eine gerade Anzahl von "-"-Multiplikatioinen immer "+" ergibt. Die Lösungsmenge einer solchen Gleichung ist leer. |
2. Basis Rechenoperationen mit Wurzeln
2.1. Teilweises Wurzelziehen
| In bestimmten Fällen ist es möglich, nur von einem Teil des Radikanten die Wurzel zu ziehen. Dies ist immer dann möglich, wenn der Radikant in Faktoren zerlegt werden kann und einer dieser Faktoren ein quadratischer Ausdruck, ein Kubikausdruck usw. ist. |
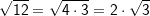 |
| Bei dieser Wurzel konnte die Zahl 12 in die beiden Faktoren 4 und 3 zerlegt werden, wobei der Faktor 4 eine Quafdratzahl ist, von der die Wurzel gezogen werden kann. |
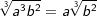 |
| Diese Kubikwurzel besteht bereits aus einem Produkt. Aus a3 kann die Kubikwurzel gezogen werden, aus b2 eben nicht. |
| Nähere Einzelheiten und Übungaufgaben siehe Kapitel „Teilweises Wurzelziehen“. |
2.2. Faktor unter die Wurzel bringen
| In manchen Fällen ist es sinnvol, zur Vereinfachung eines Wurzelterms eine Zahl, die vor einer Wurzel steht, unter die Wurzel zu schreiben. |
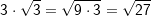 |
|
| Bei dieser Wurzel wurde die vor der Wurzel stehende Zahl 3 zunächst quadriert und mit diesem Wert unter die Wurzel geschrieben und danach das Produkt aus 9 und 3 gebildet. | |
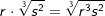 |
|
| Bei dieser Kubikwurzel wurde der vor der Wurzel stehende Ausdruck r zur dritten Potenz genommen, um dann mit dem Wert r3 unter die Wurzel geschrieben zu werden. | |
| Nähere Einzelheiten und Übungaufgaben siehe Kapitel „Faktor unter die Wurzel bringen“. |
2.3. Wurzel Nenner rationale machen
Im allgemeinen ist es unüblich bei einem Bruch eine Wurzel im Nenner stehen zu lassen. Mathematikern gefällt der Ausdruck 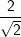 überhaupt nicht. Sie bemühen sich, die Wurzel im Nenner irgendwie zu beseitigen. überhaupt nicht. Sie bemühen sich, die Wurzel im Nenner irgendwie zu beseitigen.Das geht besonders einfach dadurch, dass man den Bruch genau mit der im Nenner stehenden Wurzel erweitert. |
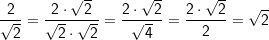 |
Zunächst wurde hier mit 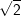 erweitert, durch ausmultiplizieren des Nenners ergibt sich die Zahl 2, die dann abschließend noch mit der im Zähler stehenden 2 gekürzt wurde. erweitert, durch ausmultiplizieren des Nenners ergibt sich die Zahl 2, die dann abschließend noch mit der im Zähler stehenden 2 gekürzt wurde. |
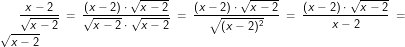 |
Zunächst wurde hier mit 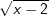 erweitert, durch ausmultiplizieren des Nenners ergibt sich der Ausdruck x-2, der dann abschließend noch mit dem im Zähler stehenden Ausdruck x-2 gekürzt wurde. erweitert, durch ausmultiplizieren des Nenners ergibt sich der Ausdruck x-2, der dann abschließend noch mit dem im Zähler stehenden Ausdruck x-2 gekürzt wurde. |
| Nähere Einzelheiten und Übungaufgaben siehe Kapitel „Wurzel Nenner rational machen“. |
2.4. Potenzdarstellung von Wurzeln
| In bestimmten Sitationen ist es erforderlich, eine Wurzel in die Potenzschreibweise zu überführen (z. B. innerhalb der Differenzialrechnug in den Ableitungen). Die Regel hierzu lautet, dass der Wurzelradikant zur Basis der Potenzschreibweise wird und die Basis mit dem Kehrwert des Wurzelexponenten potenziert wird. |
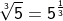 |
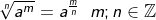 |
| Wurzeln können als Potenz dargestellt werden, indem die Wurzelbasis mit dem Quotienten aus Basisexponent und Wurzelexponent potenziert wird. |
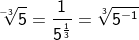 |
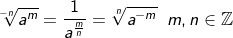 |
| Werden Wurzeln mit neagtivem Wurzelexponent oder Basisexponent als Potenz dargestellt, so entspricht die Darstellung dem Kehrwert der positiven Darstellung. |
| Nähere Einzelheiten und Übungaufgaben siehe Kapitel „Potenzdarstellung von Wurzeln“. |
| Du befindest dich hier: |
| WIKI zur Wurzelrechnung und den Wurzelgesetzen allgemein |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 15. Juli 2021 15. Juli 2021

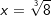
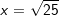
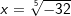
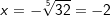 , denn
, denn 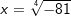
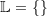
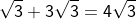
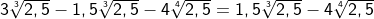
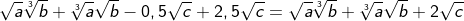
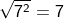
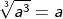
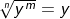 für n=m
für n=m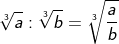

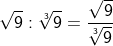

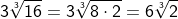
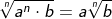
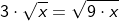
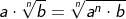
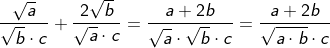
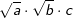 mit entsprechender Erweiterung der Zähler).
mit entsprechender Erweiterung der Zähler).