|
|
Die Funktionsklassen der Differenzialrechnung
|


Der Begriff Funktion
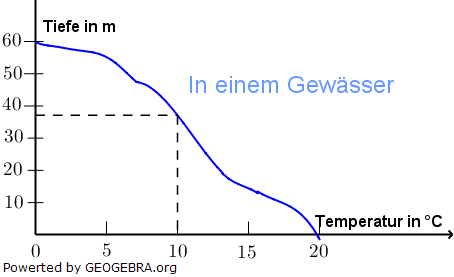
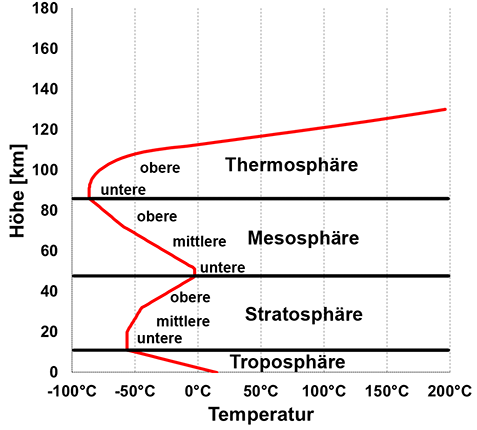
| Um uns klar zu machen, was eine Funktion (lateinisch functio) ist, betrachten wir uns die Gegenüberstellung nachfolgender Situationen. | ||||||||
  |
||||||||
|
Darstellungsformen
| Nachdem wir nun festgelegt haben, was eine Funktion überhaupt ist, müssen wir uns über die Darstellungsformen unterhalten. Hierzu kennt der Mathematiker vier Arten. Eine dieser Arten haben wir bereits in der Mittelstufe kennengelernt, nämlich die Wertetabelle. | ||||||||||||||||||||
| Wertetabelle Einer Reihe von x-Werten wird in einer Tabelle deren zugehörigen y-Werte zugeordnet, wie nachfolgendes Beispiel zeigt.
Dann gibt es als nächste Bezeichnungsform die Funktionsvorschrift f: x ⟼ 3x2+5 (Sprich der Funktionsname f bildet das Element x auf den Funktionsterm 3x2+5 ab) Als weitere Bezeichnungsform ist die Funktionsgleichung zu nennen. Funktionsgleichung f(x) = 3x2+5 (Sprich der Funktionswert f(x)=y errechnet sich aus dem Funktionsterm 3x2+5) |
||||||||||||||||||||
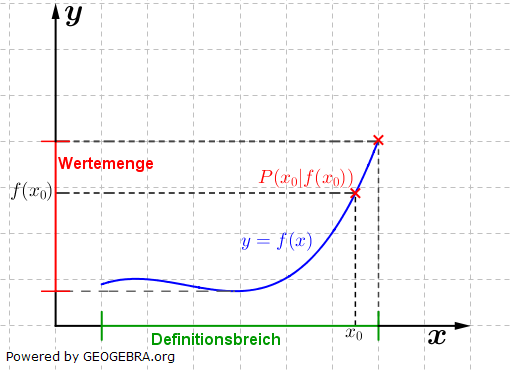 Und als bekannteste (vierte) und wohl auch einsichtigste Darstellungsform ist der Graph einer Funktion zu nennen. Und als bekannteste (vierte) und wohl auch einsichtigste Darstellungsform ist der Graph einer Funktion zu nennen.Graph von f Der Graph von f besteht aus allen Punkten P(x|y), deren Koordinaten die Gleichung y=f(x) erfüllen (Punktprobe). Die Menge aller möglichen y-Werte heißt Wertemenge von f und wird mit 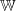 bezeichnet. bezeichnet.Die Menge aller möglichen x-Werte heißt Definitionsmenge von f und wird mit 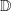 bezeichnet. bezeichnet. |
Beispiele
Funktionsklassen im Einzelnen
Betrachten wir uns nun die einzelnen Funktionsklassen.1. Lineare Funktionen
| Lineare Funktionen sind Geraden. Aus früheren Klassenstufen kennen wir schon deren allgemeine Form mit y=mx+c. Der Graph linearer Funktionen ist eine Gerade. | |
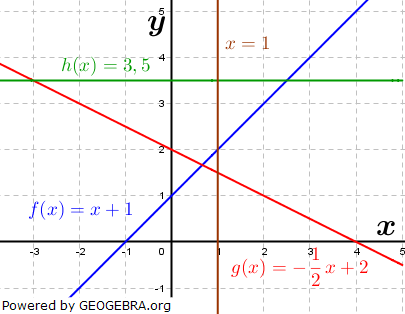 In der seitlichen Abbildung erkennen wir Geraden mit positiver Steigung, mit negativer Steigung und mit der Steigung gleich Null. Geraden mit der Steigung Null verlaufen parallel zur x-Achse. In der seitlichen Abbildung erkennen wir Geraden mit positiver Steigung, mit negativer Steigung und mit der Steigung gleich Null. Geraden mit der Steigung Null verlaufen parallel zur x-Achse. Eine Sonderform nimmt die Gleichung einer parallelen Geraden zur y-Achse ein. Diese lautet x=c mit 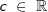 , c gibt dabei den Abstand der Geraden zur y-Achse an. , c gibt dabei den Abstand der Geraden zur y-Achse an. Aus den zuvor aufgeführten Bedingungen ergibt sich für die x-Achse selbst die Funktionsgleichung y=0 und für die y-Achse die Gleichung x=0. (Beachte zum zuletzt Gesagten: wir sprechen bei x=c nicht von einer Funktionsgleichung, da x=c keine Funktion ist, denn hier wird ja einem einzelnen Wert x=c eine unendliche Anzahl von y-Werten zugeordnet.)
|
2. Quadratische Funktionen (Parabeln)
| Quadratische Funktionen sind Kurven. Aus früheren Klassenstufen kennen wir schon deren allgemeine Form mit y=ax2+bx+c. Der Graph quadratischer Funktionen heißt Parabel. | |
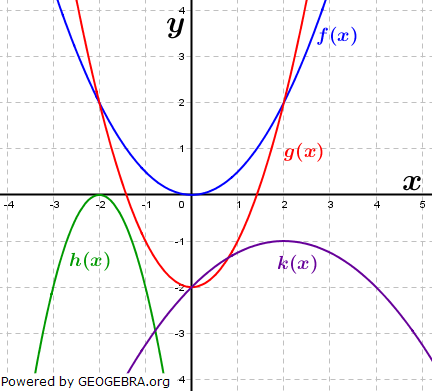 In der seitlichen Abbildung erkennen wir Parabeln die nach oben geöffnet sind (f(x) und g(x)) und solche, die nach unten geöffnet sind (h(x) und k(x)). Außerdem erkennen wir schmäler geöffnete (h(x)) als auch breiter geöffnete Parabeln (k(x)). Dieses Verhalten wird durch den Parameter a von x2 verursacht. In der seitlichen Abbildung erkennen wir Parabeln die nach oben geöffnet sind (f(x) und g(x)) und solche, die nach unten geöffnet sind (h(x) und k(x)). Außerdem erkennen wir schmäler geöffnete (h(x)) als auch breiter geöffnete Parabeln (k(x)). Dieses Verhalten wird durch den Parameter a von x2 verursacht.Wir erkennen in y-Richtung verschobene Parabeln (g(x) und k(x)). Dieses Verhalten wird durch den Parameter c verursacht. Wir erkennen in x-Richtung verschobene Parabeln (h(x) und k(x)). Dieses Verhalten wird durch den Parameter b von x verursacht.
|
3. Potenzfunktionen
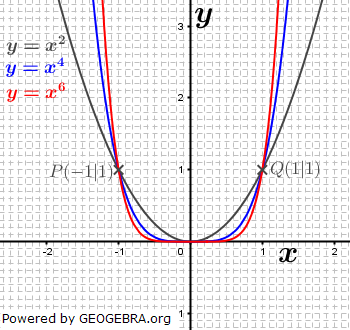
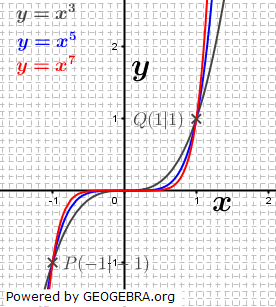
| Neben linearen und quadratischen Funktionen gibt es weitere Funktionen, wie zum Beispiel die Potenzfunktionen. Funktionen wie etwa f(x)=x3, f(x)=2x3 oder f(x)=-0,7x3 sind Potenzfunktionen 3. Grades. Die Zuordnung „3. Grades“ rührt vom Exponenten von x her. Entsprechend gibt es Potenzfunktionen 4., 5., 6. usw. Grades. Einige der besonderen Eigenschaften von Potenzfunktionen sind nachfolgend zusammengestellt.
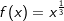 . . |
||||||||||||||||
|
||||||||||||||||
4. Ganzrationale Funktionen
| Ganzrationale Funktionen sind zusammengesetzte Funktionen, deren einzelne Glieder wiederum aus Potenzfunktionen mit ganzzahlig positivem Exponenten bestehen. Die allgemeinen Form einer Ganzrationalen Funktion lautet: | ||||
| f(x)=an⋅xn+an-1⋅xn-1+an-2⋅xn-2+...+a1⋅x+a0. | ||||
| n ist höchste Potenz, n-1 ist die um 1 verminderte höchste Potenz, n-2 die um 2 verminderte höchste Potenz usw. bis zur Potenz 1 bei a1x. Am Ende der Funktionsgleichung steht dann das absolute Glied a0. Die a-Werte in der Gleichung werden als Koeffizienten bezeichnet. Alle a sind Element von 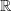 . Die Indices von an, a(n-1), a(n-2) usw. verweisen auf die Teilfunktion mit dem entsprechenden n als Exponenten. . Die Indices von an, a(n-1), a(n-2) usw. verweisen auf die Teilfunktion mit dem entsprechenden n als Exponenten. |
||||
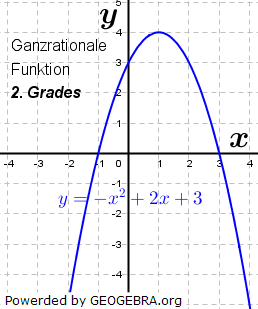 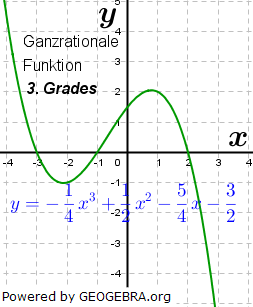 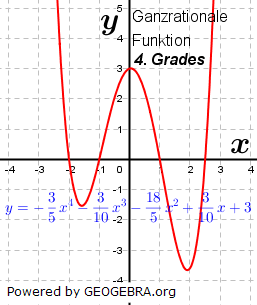 |
||||
| Entsprechend der höchsten Potenz n von x wird den ganzrationalen Funktionen ein Grad zugesprochen. Ist n=3, so handelt es sich um eine ganzrationale Funktion 3. Grades. Ist n=4, so handelt es sich um eine ganzrationale Funktion 4. Grades. Ist n=5, so handelt es sich … Ganzrationale Funktionen werden auch Polynome oder (seltener für Funktionen mit einem Grad größer n=2) Parabeln genannt. Auch die bereits behandelten lineare Funktionen g mit g(x)=mx+c und die quadratischen Funktionen p mit p(x)=ax2+bx+c zählen zu den ganzrationalen Funktionen. Erstere ist vom Grad 1, letztere vom Grad 2. |
||||
|
||||
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

 für die zulässigen x-Werte.
für die zulässigen x-Werte.  .
.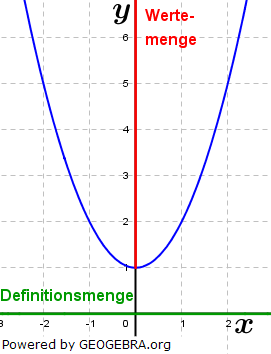 Die Funktion ist für alle reellen Zahlen definiert, die Definitionsmenge ist also
Die Funktion ist für alle reellen Zahlen definiert, die Definitionsmenge ist also 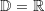 .
. die Wertemenge von f.
die Wertemenge von f. bzw.
bzw. 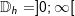
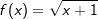 .
.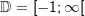
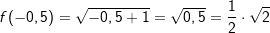
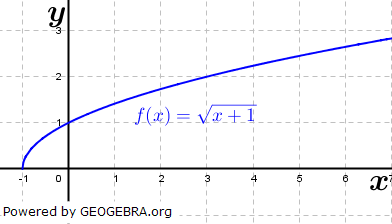
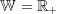 .
.