 |
Gebrochen-rationale Funktionen - Level 2 - Fortgeschritten - Blatt 1 |
| Dokument mit 26 Aufgaben |
Aufgabe A1 (6 Teilaufgaben)
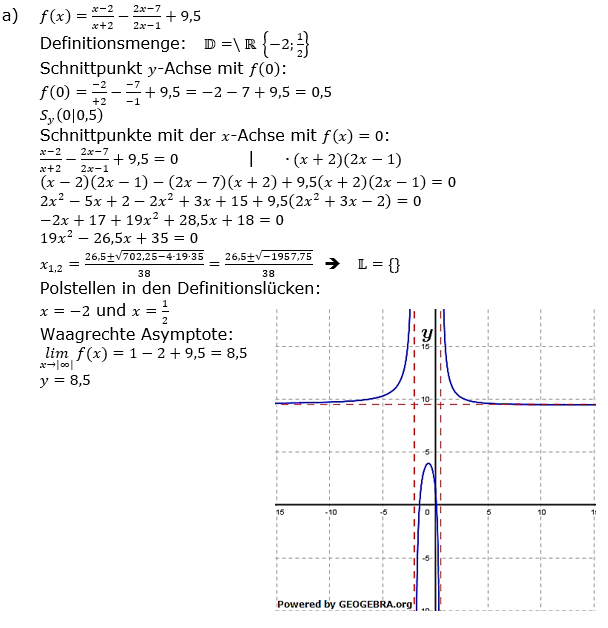
Bestimme die Definitionsmenge, Schnittpunkte mit den Koordinatenachsen, Polstellen und das asymptotische Verhalten im Unendlichen nachfolgender gebrochen-rationaler Funktionen f mit  . |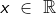
|||
| a) |  |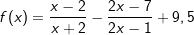
b) |  |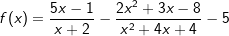
| c) |  |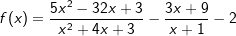
d) |  |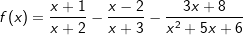
| e) |  |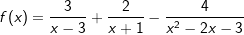
f) | |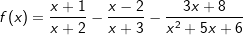
 Eine Frage stellen... |
Definitionsmenge ist stets  mit Ausnahme der Zahlen, die den/die Nenner der Funktion zu Null werden lassen.Schnittpunkt mit der y-Achse über f(0). Schnittpunkt(e) mit der x-Achse über f(x)=0. Polstellen (senkrechte Asymptoten) in den Definitionslücken der Funktion. Waagrechte Asymptoten über Grenzwertbetrachtung für x→|∞|. |
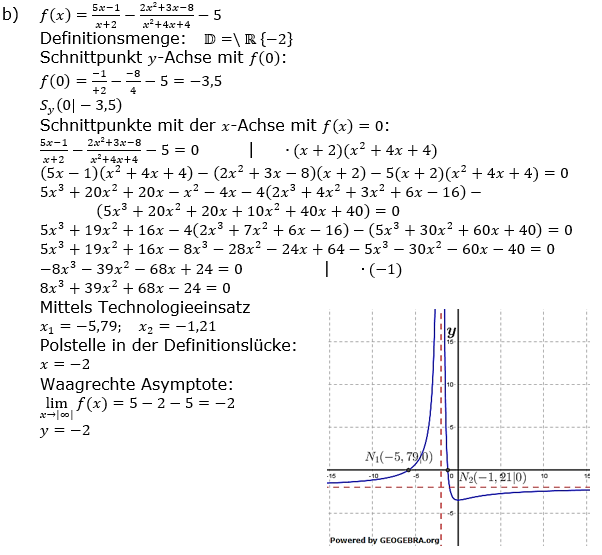
Fehler melden...Aufgabe A2 (6 Teilaufgaben)
| Bestimme die Definitionsmenge, Schnittpunkte mit den Koordinatenachsen, Polstellen und das asymptotische Verhalten im Unendlichen nachfolgender gebrochen-rationaler Funktionen f mit . |
|||
| a) |  |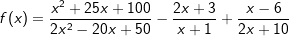
b) |  |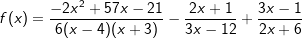
| c) |  |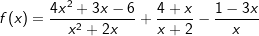
d) |  |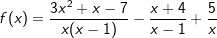
| e) |  |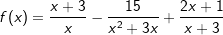
f) |  |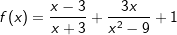
| Eine Frage stellen... |
Aufgabe A3 (5 Teilaufgaben)
| Bestimme den Definitionsbereich und die Schnittpunkte – falls vorhanden – der Funktionen f und h mit . |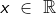
||
| a) |  |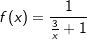
 |
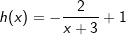| b) |  |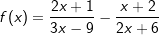
 |
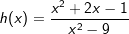| c) |  |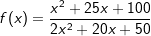
 |
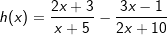| d) |  |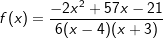
 |
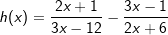| e) |  |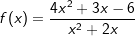
 |
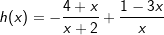| Eine Frage stellen... |
Aufgabe A4 (5 Teilaufgaben)
| Bestimme den Definitionsbereich und die Schnittpunkte – falls vorhanden – der Funktionen f und h mit . |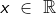
||
| a) |  |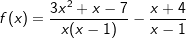
 |
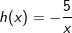| b) |  |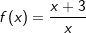
 |
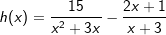| c) |  |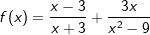
 |
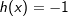| d) |  |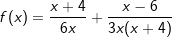
 |
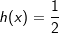| e) |  |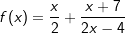
 |
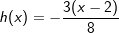| Eine Frage stellen... |
Aufgabe A5 (4 Teilaufgaben)
| Bestimme den Definitionsbereich und die Schnittpunkte – falls vorhanden – der Funktionen f und h mit . |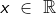
||
| a) |  |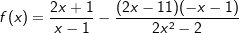
 |
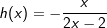| b) |  |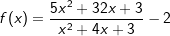
 |
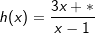| c) |  |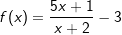
 |
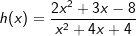| d) |  |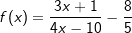
 |
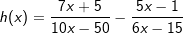| Eine Frage stellen... |
| Du befindest dich hier: |
| Gebrochen-rationale Funktionen Level 2 - Fortgeschritten - Blatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 26. Dezember 2022 26. Dezember 2022
