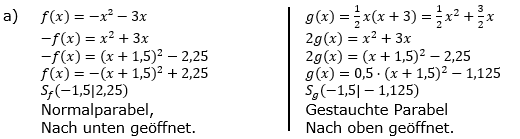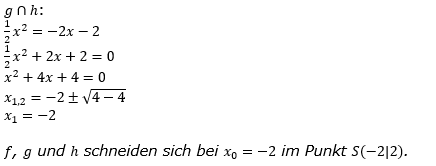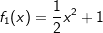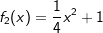|
Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 3 |
| Dokument mit 25 Aufgaben |
Aufgabe A1 (4 Teilaufgaben)
| Die Tabelle zeigt eine Wertetabelle für zwei Funktionen f und g. Beantworte folgende Fragen mit Hilfe der Wertetabelle. | ||||
| a) | Wo schneiden Kf und Kg die x–Achse? | x | f(x) | g(x) |
| b) | Wo liegen die Scheitelpunkte von Kf und Kg? | -3 | -3,5 | 4 |
| c) | Welcher Zusammenhang besteht zwischen Kf und Kg? | -2 | 0,5 | 0 |
| d) | Gib eine Funktionsgleichung für f und g an. | -1 | 2,5 | -2 |
| 0 | 2,5 | -2 | ||
| 1 | 0,5 | 0 | ||
| 2 | -3,5 | 4 | ||
| |
Aufgabe A2 (4 Teilaufgaben)
Gegeben ist die Funktion f mit 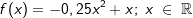 . . |
|
| a) | Wo hat die zugehörige Parabel ihren Scheitelpunkt? Zeichne K. |
| b) | H ist eine Ursprungsgerade durch den Punkt P(-2|3). Berechne die Koordinaten der Schnittpunkte von Parabel K und Gerade H. |
| c) | Welche Tangente an die Parabel K ist parallel zur Geraden mit y=-1,5x+18? Bestimme die Koordinaten des Berührpunktes. |
| d) | Durch eine Verschiebung der Parabel K entsteht die Parabel G. G soll die x–Achse berühren. Bestimme den zugehörigen Funktionsterm. Erläutere deine Vorgehensweise. |
| |
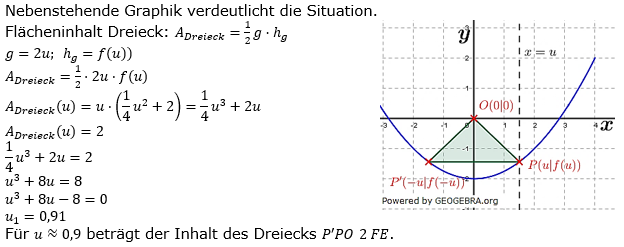
Aufgabe A3
Gegeben ist die Funktion f mit 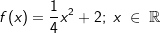 , ihr Graph sei K. , ihr Graph sei K.Der Punkt B(u|f(u)) auf dem Graphen K ist für 1 < u < 2 der Eckpunkt eines achsensymmetrischen Dreiecks mit der Spitze im Ursprung. Zeichne das Dreieck für u=1 in ein Achsenkreuz ein. Bestimme den Flächeninhalt in Abhängigkeit von u. Für welchen Wert von u hat das Dreieck eine Fläche von 2 FE? |
| |
Aufgabe A4 (2 Teilaufgaben)
Gegeben sind die quadratischen Funktionen f und g mit 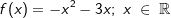 und und 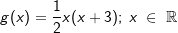 . . |
|
| a) | Mache Aussagen über die gegenseitige Lage der beiden Schaubilder K von f und G von g. |
| b) | Verschiebe die Parabel G von g in y–Richtung so, dass die verschobene Parabel das Schaubild K von f berührt. Bestimme die Koordinaten des Berührpunktes. |
| |
Aufgabe A5
| Gegeben ist die Funktion g mit g(x)=x2-2; x ∈ R. Wie entsteht das Schaubild von f aus dem Schaubild von g? | |||
| a) | f(x)=g(x+2) | b) | f(x)=g(-x) |
| c) | f(x)=0,5g(x)+1 | ||
| |
Aufgabe A6
Gegeben sind die Funktionen f und g durch f(x)=x2-2 und 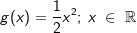 . Durch den Scheitel der Parabel K von f verläuft das Schaubild H einer linearen Funktion mit dem Anstieg -2. . Durch den Scheitel der Parabel K von f verläuft das Schaubild H einer linearen Funktion mit dem Anstieg -2.Gib die Argumente (x-Werte) an, für die die Funktionswerte von f, g und h jeweils gleich 0 bzw. größer als 3 sind. Haben die drei Graphen von f, g und h einen gemeinsamen Punkt? |
| |
Lösungshilfe A6
| Bestimme zunächst den Scheitelpunkt der Parabel K und stelle die Funktionsgleichung der Geraden H durch den Scheitelpunkt mit der Steigung m=-2 auf. Bestimme nun die Nullstellen für f, g und h sowie die Intervalle, in denen die Funktionswerte von f, g und h größer als 3 sind. Bestimme abschließend die Schnittpunkte von f ∩ g, f ∩ h und g ∩ h und prüfe, ob es einen gemeinsamen Schnittpunkt gibt. |
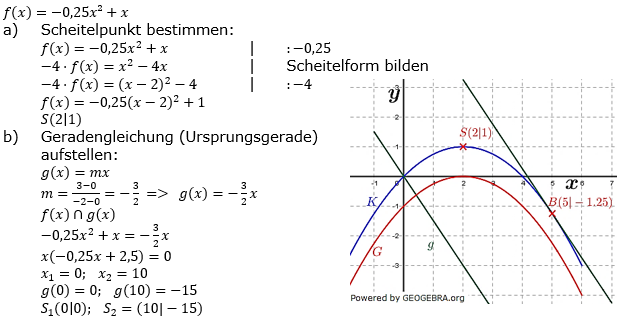
Aufgabe A7
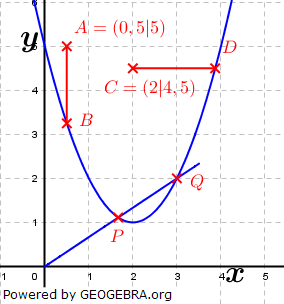 Die eingezeichnete Strecke Die eingezeichnete Strecke 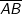 beginnt im angegebenen Punkt A und endet am Graph K der Funktion f. beginnt im angegebenen Punkt A und endet am Graph K der Funktion f.Berechne die Längen der eingezeichneten Strecken 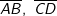 und und 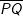 . . |
| |
Lösungshilfe A7
| Bestimme zunächst die Funktionsgleichungen der beiden Graphen in der Grafik. Bestimme dann die Koordinaten der Punkte B und D auf der Parabel, sowie die der Punkte P und Q als Schnittpunkte zwischen Parabel und Gerade. Abstände zwischen zwei Punkte errechnen wir mit dem Satz des Pythagoras. |
Aufgabe A8
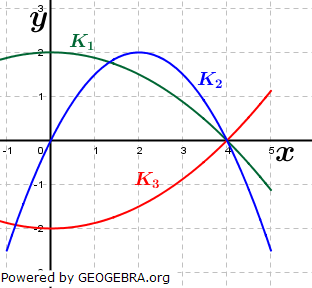 Welches Schaubild der nebenstehenden Abbildung passt zu folgender Beschreibung: Welches Schaubild der nebenstehenden Abbildung passt zu folgender Beschreibung: Die Parabel ist symmetrisch zur Geraden x=2 und schneidet die x-Achse in 4. Begründe deine Wahl. |
| |
Aufgabe A9 (8 Teilaufgaben)
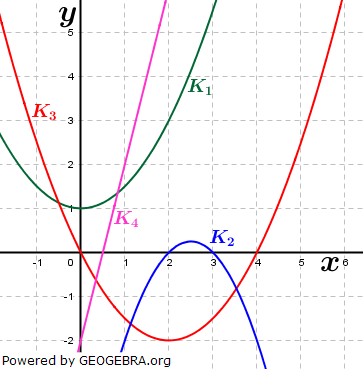 Entscheide, welche Kurve zu welchem Funktionsterm passt. Begründe, indem du jeweils eine Eigenschaft angibst. Entscheide, welche Kurve zu welchem Funktionsterm passt. Begründe, indem du jeweils eine Eigenschaft angibst.
|
| |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 3 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021