 |
Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 2 |
| Dokument mit 24 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
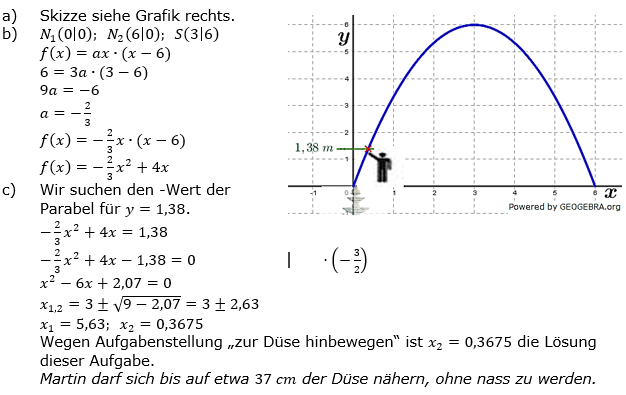
| Der Wasserstrahl eines Springbrunnens hat eine Höhe von 6 m und eine Weite von 6 m. Martin hat Lust unter dem Wasserstrahl durchzulaufen. | |
| a) | Wähle ein geeigneters Koordinatensystem und skizziere den Wasserstrahl. |
| b) | Bestimme den zugehörigen Funktionsterm. |
| c) | Martin ist 1,38 m groß. Wie weit darf er sich zur Düse hinbewegen, ohne nass zu werden? |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (4 Teilaufgaben)
| Bestimme die Gleichung der Parabel, wenn folgendes bekannt ist: | |
| a) | Die Parabel berührt die x–Achse in x=-36 und verläuft durch A(-5|-7). |
| b) | Die Parabel schneidet die x–Achse in 2 und -1 und verläuft durch A(1|-2). |
| c) | Eine verschobene Normalparabel berührt die x–Achse bei x=-2. |
| d) | Die Parabel verläuft symmetrisch zur y–Achse durch die Punkte A(1|0,5) und B(-2|-5,5). |
| Eine Frage stellen... |
Aufgabe A3 (4 Teilaufgaben)
| Bestimme die Gleichung der Parabel, wenn folgendes bekannt ist: | |
| a) | Die Parabel berührt die x–Achse in x=-3 und verläuft durch A(-5|-7). |
| b) | Die Parabel schneidet die x–Achse in -2 und 1 und verläuft durch A(-1|2). |
| c) | Eine verschobene Normalparabel berührt die x–Achse bei x=2. |
| d) | Die Parabel verläuft symmetrisch zur y–Achse durch die Punkte A(-1|-0,5) und B(2|5,5). |
| Eine Frage stellen... |
Aufgabe A4
| Für eine quadratische Funktion f gilt f(-2)=3=f(2). Welche Eigenschaft hat das Schaubild von f? Bestimme einen Funktionsterm. Ist der Graph von f festgelegt, wenn der Graph die Form einer Normalparabel hat? |
| Eine Frage stellen... |
Aufgabe A5
| Eine Parabel hat den Scheitel S(1|4) und verläuft durch den Ursprung. Bestimme die Parabelgleichung. |
| Eine Frage stellen... |
Aufgabe A6 (2 Teilaufgaben)
| Gegeben ist die Funktion f mit f(x)=x²+bx+c. Mache Aussagen über b und c, wenn gilt: | |
| a) | f hat eine Nullstelle in x=0. |
| b) | Die Nullstellen von f unterscheiden sich nur im Vorzeichen. |
| Eine Frage stellen... |
Aufgabe A7
| Für eine quadratische Funktion f mit f(x)=ax²+bx+c gilt f(0)=5 und f(1)=2. Welche Beziehung besteht zwischen a und b? Bestimme a und b, wenn x=3 Nullstelle von f ist. |
| Eine Frage stellen... |
Aufgabe A8 (3 Teilaufgaben)
| Gib jeweils zwei Funktionsterme von verschiedenen quadratischen Funktionen an, deren Schaubilder | |
| a) | keinen Schnittpunkt mit der x–Achse haben. |
| b) | zwei Schnittpunkte mit der x–Achse haben. |
| c) | den Scheitel S(-2|0) besitzen. |
| Eine Frage stellen... |
Aufgabe A9
| Gegeben sind die Funktionen f und g durch f(x)=ax²+bx+3 und g(x)=2x-1. Die Funktionswerte von f und g stimmen in x=-1 und x=0,5 überein. Bestimme a und b. |
| Eine Frage stellen... |
| Aus dem Text heraus müssen wir interpretieren, dass sich f und g schneiden, nämlich in x1=-1 und x2=0,5. Da die Funktionsgleichung von g vollständig gegeben ist, können wir die zugehörigen y-Werte errechnen. Damit haben wir zwei Punkte der Parabel. Durch Punktproben können wir dann a und b ermitteln. |
Aufgabe A10
| Eine Parabel 2. Ordnung schneidet die x–Achse in -5 und 5. Die zugehörige Funktion ist damit nicht eindeutig bestimmt. Gib die Funktionsterme von zwei möglichen Funktionen an. Zeige, dass die Schaubilder symmetrisch zur y–Achse sind. |
| Eine Frage stellen... |
Aufgabe A11
| Das Schaubild einer quadratischen Funktion f geht durch die Punkte P(-2|1), Q(-4|4) und R(6|9). Bestimme f(x). |
| Eine Frage stellen... |
Aufgabe A12
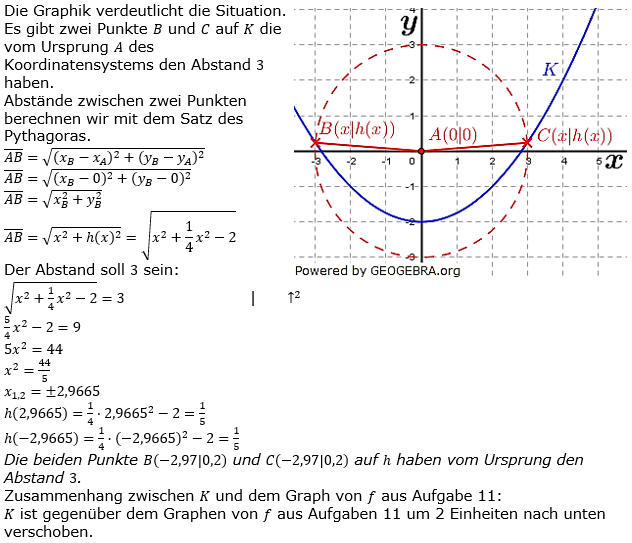
Skizziere das Schaubild K der Funktion h mit 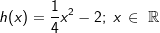 in ein geeignetes Koordinatensystem und kennzeichne die markanten Punkte.Welche Punkte auf K haben vom Ursprung einen Abstand von 3? Welcher Zusammenhang besteht zwischen K und dem Graphen von f aus Aufgabe 11? |
| Eine Frage stellen... |
Aufgabe A13
| Eine Gerade g geht durch die Punkte T1(-1|-1,75) und T2(-4|-4). Für welche Werte von x gilt: K aus Aufgabe 12 verläuft unterhalb von g? Erläutere deinen Lösungsweg. |
| Eine Frage stellen... |
| Zunächst müssen wir über die beiden gegebenen Punkte T1 und T2 die Funktionsgleichung der Geraden aufstellen. Wir bestimmen dann die Schnittpunkte dieser Geraden mit der quadratischen Funktion f aus Aufgabe 12. Über die entstehenden Schnittpunkte können wir dann entscheiden, in welchen Intervallen g oberhalb bzw. unterhalb von K verläuft. |
Aufgabe A14
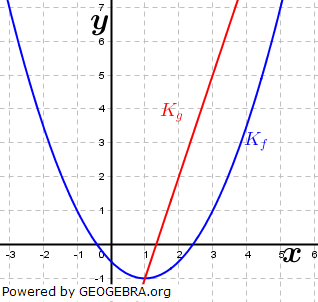 Die Abbildung zeigt den Graphen Kf einer quadratischen Funktion sowie Kg einer linearen Funktion.Berechnen Sie die Koordinaten der Schnittpunkte von Kf und Kg. |
| Eine Frage stellen... |
| Aus der gegebenen Graphik heraus müssen wir die Funktionsgleichungen für Kf und Kg bestimmen. Durch Gleichsetzung der beiden Funktionsgleichungen können wir die Schnittpunkte von f und g bestimmen. |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 2 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 26. September 2022 26. September 2022
