 |
|
Integralrechnung | Begriffe und Themengebiete |
|


1. Integralrechnung - Einführung
| Wie überall in der Mathematik gibt es zu den einzelnen Rechenarten jeweils deren Umkehrrechenarten. So ist die Subtraktion die Umkehrrechenart der Addition, die Division die Umkehrrechenart der Multiplikation, die Potenzierung hat gar zwei Umkehrrechenarten, das Wurzelziehen und das Logarithmieren, je nachdem, ob die Unbekannte x die Basis der Potenz darstellt (f(x)=xa) oder gar der Exponent selbst ist (f(x)=ax). |
| Die Integralrechnung ist die Umkehrrechenart der Differentialrechnung. Sie ist neben der Differentialrechnung der wichtigste Zweig der mathematischen Disziplin der Analysis. Sie ist aus dem Problem der Flächen- und Volumenberechnung entstanden. Das Integral ist ein Oberbegriff für das unbestimmte und das bestimmte Integral. Die Berechnung von Integralen heißt Integration. Der in der Schule sehr häufig genannte Begriff “Aufleiten” ist sachlich falsch und auf jeden Fall zu vermeiden. |
1.1. Geschichtliches
| Flächenberechnungen werden seit der Antike untersucht. Im 5. Jahrhundert vor Christus entwickelte Eudoxos von Knidos nach einer Idee von Antiphon die Exhaustionsmethode, die darin bestand, Verhältnisse von Flächeninhalten mittels enthaltener oder überdeckender Polygone abzuschätzen. Er konnte durch diese Methode sowohl Flächeninhalte als auch Volumina einiger einfacher Körper bestimmen. Archimedes (287–212 v. Chr.) verbesserte diesen Ansatz, und so gelang ihm die exakte Bestimmung des Flächeninhalts einer von einem Parabelbogen und einer Sekante begrenzten Fläche ohne Rückgriff auf |  Gottfried Wilhelm Leibnitz (* 1. Juli 1646 in Leipzig; † 14. November 1716 in Hannover) Quelle: commons.wikimedia.org |
den Grenzwertbegriff, der damals noch nicht vorhanden war; dieses Ergebnis lässt sich leicht in das heute bekannte Integral einer quadratischen Funktion umformen. Zudem schätzte er das Verhältnis von Kreisumfang zu Durchmesser, π, als Wert zwischen 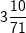 und und 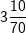 ab. ab. |
|
| Diese Methode wurde auch im Mittelalter benutzt. Im 17. Jahrhundert stellte Bonaventura Francesco Cavalieri das Prinzip von Cavalieri auf, wonach zwei Körper das gleiche Volumen haben, wenn alle parallelen ebenen Schnitte den gleichen Flächeninhalt haben. Johannes Kepler benutzte in seinem Werk Astronomia Nova (1609) bei der Berechnung der Marsbahn Methoden, die heute als numerische Integration bezeichnet werden würden. Er versuchte ab 1612, den Rauminhalt von Weinfässern zu berechnen. 1615 veröffentlichte er die Stereometria Doliorum Vinariorum („Stereometrie der Weinfässer“), später auch als Kepler’sche Fassregel bekannt. | |
| Ende des 17. Jahrhunderts gelang es Isaac Newton und Gottfried Wilhelm Leibniz unabhängig voneinander Kalküle zur Differenzialrechnung zu entwickeln und so den Fundamentalsatz der Analysis zu entdecken. Ihre Arbeiten erlaubten das Abstrahieren von rein geometrischer Vorstellung und werden deshalb als Beginn der Analysis betrachtet. Bekannt wurden sie vor allem durch das Buch des Adligen Guillaume François Antoine, Marquis de L’Hospital, der bei Johann Bernoulli Privatunterricht nahm und dessen Forschung zur Analysis so publizierte. Der Begriff Integral geht auf Johann Bernoulli zurück. |  Sir Isaac Newton (*4. Januar 1643 in Wools Thorpe-by-Colsterworth in Lincolnshire; † 31. März 1727. in Kensington) Quelle: commons.wikimedia.org |
| Im 19. Jahrhundert wurde die gesamte Analysis auf ein solideres Fundament gestellt. 1823 entwickelte Augustin-Louis Cauchy erstmals einen Integralbegriff, der den heutigen Ansprüchen an Stringenz genügt. Später entstanden die Begriffe des Riemann-Integrals und des Lebesgue-Integrals. Schließlich folgte die Entwicklung der Maßtheorie Anfang des 20. Jahrhunderts. | |
1.2. Mathematisches Zeichen
Das Integralzeichen 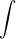 ist aus dem Buchstaben langes s („ſ“) als Abkürzung für das Wort Summe, lateinisch ſumma, entstanden. Diese symbolische Schreibweise von Integralen geht auf Gottfried Wilhelm Leibniz zurück. Für das Integralzeichen gibt es eine Reihe von Abwandlungen, unter anderem für Mehrfachintegrale, Kurvenintegrale, Oberflächenintegrale und Volumenintegrale. ist aus dem Buchstaben langes s („ſ“) als Abkürzung für das Wort Summe, lateinisch ſumma, entstanden. Diese symbolische Schreibweise von Integralen geht auf Gottfried Wilhelm Leibniz zurück. Für das Integralzeichen gibt es eine Reihe von Abwandlungen, unter anderem für Mehrfachintegrale, Kurvenintegrale, Oberflächenintegrale und Volumenintegrale. |
2. Das unbestimmte Integral
| Das unbestimmte Integral einer Funktion ordnet dieser eine Menge von Funktionen zu, deren Elemente Stammfunktionen genannt werden. Diese zeichnen sich dadurch aus, dass ihre ersten Ableitungen mit der Funktion, die integriert wurde, übereinstimmen. Der Hauptsatz der Differential- und Integralrechnung besagt, dass (bestimmte) Integrale aus Stammfunktionen berechnet werden können. |
| Im Gegensatz zur Differentiation existiert für die Integration auch elementarer Funktionen kein einfacher und kein alle Fälle abdeckender Algorithmus. Integration erfordert trainiertes Raten, Benutzung spezieller Umformungen (Integration durch Substitution, partielle Integration), Nachschlagen in einer Integraltafel oder Benutzung spezieller Computer-Software. Oft erfolgt die Integration nur näherungsweise mittels so genannter numerischer Quadratur. |
| Ähnlich den unterschiedlichen Regeln der Differentialrechnung, wie z. B. Konstanten- Potenz- Summen-, Produkt-, Quotienten-, Ketten- und Umkehrregel gibt es auch entsprechende |
| Ableiten ist Handwerk. Integration ist Kunst. |
3. Das bestimmte Integral
| Das bestimmte Integral einer Funktion ordnet dieser einen Zahlwert zu. Bildet man das bestimmte Integral einer reellen Funktion in einer Variablen, so lässt sich das Ergebnis im zweidimensionalen Koordinatensystem als Flächeninhalt der Fläche, die zwischen dem Graphen der Funktion, der x-Achse und den begrenzenden Parallelen zur y-Achse liegt, deuten. Hierbei zählen Flächenstücke unterhalb der x-Achse negativ. Man spricht vom orientierten Flächeninhalt. Diese Konvention wird gewählt, damit das bestimmte Integral eine lineare Abbildung ergibt, was sowohl für theoretische Überlegungen als auch für konkrete Berechnungen eine zentrale Eigenschaft des Integralbegriffs darstellt. In der Technik benutzt man zur näherungsweisen Flächenbestimmung so genannte Planimeter, bei welchen die Summierung der Flächenelemente kontinuierlich erfolgt. Der Zahlenwert der so bestimmten Fläche kann an einem Zählwerk abgelesen werden, welches zur Erhöhung der Ablesegenauigkeit mit einem Nonius versehen ist. Chemiker pflegten früher Integrale beliebiger Flächen mit Hilfe einer Analysenwaage oder Mikrowaage zu bestimmen: Die Fläche wurde sorgfältig ausgeschnitten und gewogen, ebenso ein genau 10 cm X 10 cm großes Stück des gleichen Papiers; eine Dreisatzrechnung führte zum Ergebnis. |
4. Integrationsregeln
| Ähnlich den verschiedenen Ableitungsregeln werden, unabhängig, ob ein unbestimmtes Integral oder ein bestimmtes Integral ermittelt werden soll, für die Berechnung einer Stammfunktion Integrationsregeln benötigt. Die verschiedenen Integrationsregeln seien hier nur namentlich aufgeführt. Wie sie zu behandeln sind erfolgt in den Untermenüs des unbestimmten Integrals. |
|||
| Die wichtigsten Integrationsregeln lauten: | |||
| 1. | Die „Nullregel“ Die Nullregel besagt, dass das Integral von Null eine Konstante ist. 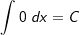 |
||
| 2. | Die „1-Regel“ Die 1-Regel besagt, dass 1 zu x wird. 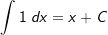 |
||
| 3. | Die „Konstantenregel“ Die Konstantenregel besagt, dass eine Konstante 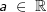 erhalten bleibt. erhalten bleibt.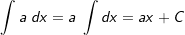 |
||
| 4. | Die „Potenzregel“ Die Potenzregel lautet: 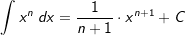 mit mit 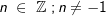 und zusätzlich und zusätzlich 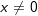 falls n<-1. falls n<-1. |
||
| 5. | Die „erweiterte Potenzregel“ Für die Potenzfunktion f(x)=xq mit 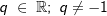 und x > 0 gilt: und x > 0 gilt: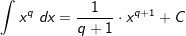 . . |
||
| 6. | Die „Faktorregel“ Es sei f eine stetige Funktion. Dann gilt: 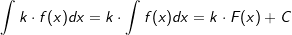 . . |
||
| 7. | Die „Summenregel“ Es seien f und g stetige Funktionen. Dann gilt: 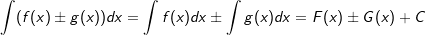 . . |
||
| Zu den komplexeren Integrationsregeln – hier nur namentlich aufgeführt, für detailliertere Informationen siehe „Das unbestimmte Integral – Stammfunktion“, zählen: | |||
| 8. | Die „lineare Substitution“ | ||
| 9. | Die „nichtlineare Substitution“ | ||
| 10. | Die „partielle Integration“ | ||
| 11. | Die „Partialbruchzerlegung“ | ||
| Dennoch bilden die hier aufgeführten Regeln nicht alle Möglichkeiten zur Findung einer Stammfunktion F von f ab. Es gibt viele Funktionen f, zu denen man nur grafisch zu einer Strammfunktion F kommen kann. Da die aufgeführten 11 Integrationbsregeln aber auch teilweise sehr komplexe Rechenschritte nach sich ziehen, existieren sogenannte „Integrationstafeln“, um ein Problem nicht jedesmal von Neuem aufrollen zu müssen. Eine der umfangreichsten Integrationstafeln ist die von Lothar Papula, einem deutschen Mathematiker, Hochschullehrer und Autor zahlreicher mathematischer Lehrbücher. Seine sechs Bände der Reihe „Mathematik für Ingenieure und Naturwissenschaftler“ erreichten im April 2008 eine Auflage von einer Million. Über diesen Link „Tabelle der Grundintegrale“ kann Papulas Integrationstabelle bestehend aus 36 Seiten mit mehr als 400 Grundintegralen heruntergeladen werden. |
|||
| Die nachfolgende Tabelle zeigt die wichtigsten Grundintegrale. | |||
| 1. | 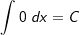 |
2. | 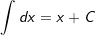 |
| 3. | 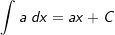 |
4. | 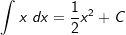 |
| 5. | 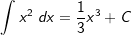 |
6. | 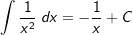 |
| 7. | 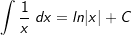 |
8. | 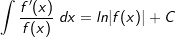 |
| 9. | 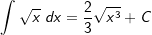 |
10. | 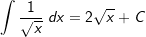 |
| 11. | 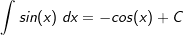 |
12. | 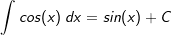 |
| 13. | 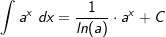 |
14. | 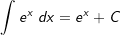 |
| 15. | 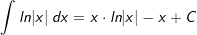 |
||
5. Uneigentliche Integrale
| Uneigentliche Integrale sind Integrale, deren untere bzw. obere Grenze unendlich groß ist. Auch Integrale, bei denen beide Grenzen unendlich groß sind, gehören zu den uneigentlichen Integralen. Integrale mit unendlichem Integrationsgebiet, entweder einseitig oder beidseitig, nennen wir „Uneigentliche Integrale der 1. Art“. |
Es gibt aber auch Funktionen, die innerhalb oder auch am Rande ihres Definitionsbereiches eine oder mehrere Singularitäten aufweisen. Ein typisches Beispiel hierfür ist die Funktion f mit 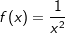 . Da f für x0=0 nicht definiert ist, ist es (zunächst) auch nicht möglich, das Integral . Da f für x0=0 nicht definiert ist, ist es (zunächst) auch nicht möglich, das Integral 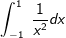 nach den uns bekannten Integrationsregeln zu lösen. Integrale, deren Funktionsgleichung eine Definitionslücke aufweisen, nennen wir „Uneigentliche Integrale der 2. Art“. nach den uns bekannten Integrationsregeln zu lösen. Integrale, deren Funktionsgleichung eine Definitionslücke aufweisen, nennen wir „Uneigentliche Integrale der 2. Art“.Weiterführende Information mit Beispielen sind im WIKI „Uneigentliches Integral“ aufgeführt. |
6. Integral und Mittelwert
| Der Flächeninhalt unter einem Graphen kann auch dazu dienen, einen Mittelwert zu bestimmen. In der Statistik werden ja Mittelwerte dadurch gebildet, dass wir endlich viel gemessene Werte addieren und diese Summe dann durch die Anzahl der Messungen dividieren. Weiterführende Information mit Beispielen sind im WIKI „Integral und Mittelwert“ aufgeführt. |
7. Integral und Rauminhalt
| Rotationskörper wird in der Geometrie ein Körper genannt, dessen Oberfläche durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet wird. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Ein bekannter Rotationskörper ist der Torus. Er wird durch die Rotation eines Kreises gebildet. Auch Kegel und Zylinder sind Rotationskörper. Das Volumen und die Oberfläche werden mit den sogenannten Guldinschen Regeln (benannt nach dem Mathematiker und Astronomen Paul Guldin) errechnet. Bereits in der Antike waren diese als Bary-zentrische Regeln bzw. Zentrobarische Regel bekannt und wurden vom griechischen Mathematiker Pappos von Alexandria beschrieben. In der heutigen Mathematik erfolgt die Berechnung von Rotationsvolumina mit Hilfe des bestimmten Integrals. Dabei unterscheiden wir zwischen Rotation um die x-Achse und Rotation um die y-Achse. Weiterführende Information mit Beispielen sind im WIKI „Integral und Rauminhalt“ aufgeführt. |
8. Mehrfachintegrale
| Mehrfachintegrale sind eine andere Art der Integralrechnung. Man spricht hier von „Bereichsintegralen“, von Flächen-, Volumen-, Massen- u.a.m. Bereichen. Die generelle Darstellung eines Integrals schreiben wir dann so: | |
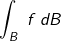 B = Bereich, B = Bereich, |
|
| sprich das Integral einer Funktion bezüglich eines Bereiches. Betrachten wir uns zunächst einen Bereich „Fläche“. Bislang haben wir die Berechnung einer Fläche über das bestimmte Integral kennengelernt, nämlich |
|
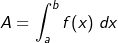 . . |
|
| Jetzt ist das Produkt aber f(x)∙dx eine winzige Fläche im zweidimensionalen Bereich (x und y) und das Integral summiert lediglich all die kleinen Flächen im Intervall I=[a;b] auf. Mit der Definition des Bereiches „Fläche“ ließe sich dieses uns bekannte Integral auch schreiben zu | |
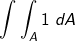 mit dA=dx⋅dy. mit dA=dx⋅dy. |
|
| Legen wir nun den Bereich „Volumen“ fest, so benötigen wir neben der Fläche ja noch eine dritte Dimension, in der Regel mit z bezeichnet. Damit erhalten wir die Koordinaten x, y und z und können schreiben | |
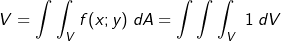 mit dV=dx⋅dy⋅dz. mit dV=dx⋅dy⋅dz. |
|
| Die Bereichsdefinition ließe sich fortsetzen mit dem Bereich „Masse“: | |
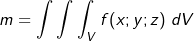 |
|
| In der Technik und Physik existieren noch andere Bereiche nämlich | |
| Arbeit: | 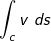 (Kurvenintegral) (Kurvenintegral) |
| Fluss: | 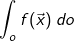 (Oberflächenintegral) (Oberflächenintegral) |
| Weiterführende Information mit Beispielen sind im WIKI „Mehrfachintegrale“ aufgeführt. | |
| Du befindest dich hier: |
| Integralrechnung | Begriffe und Themengebiete |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 09. Oktober 2021 09. Oktober 2021



