 |
Ähnlichkeitsbeweis Kathetensatz des Euklid |
Aufgabenstellung
Beweise den Kathetensatz auf zwei verschiedene Arten, einmal als Ähnlichkeitsbeweis sowie auf eine andere Art.
|
Beweisführung Ähnlichkeit
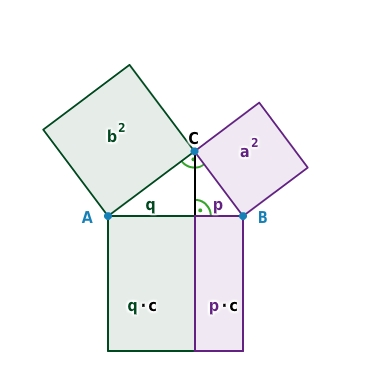
| Der Kathetensatz des Euklid lautet: In einem rechtwinkligen Dreieck ABC mit rechtem Winkel im Punkt C und Hypotenusenabschnitten p und q gilt: a2=p⋅c und b2=q⋅c. Dividiert man die Gleichungen des Kathetensatzes einmal durch die jeweilige Kathete und anschließend durch den entsprechenden Hypotenusenabschnitt, erhält man eine Verhältnisgleichung wie folgt: |
 |
||
| a2=p⋅c | | | :p | |
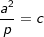 |
|||
| b2=q⋅c | | | :q | |
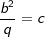 |
|||
| somit gilt: | |||
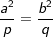 |
|||
| Da ähnlichen Figuren streckenverhältnistreu sind, zwängt sich ein Beweis des Kathetensatzes über Ähnlichkeit geradezu auf. Im nachfolgenden führen wir den Beweis in 5 Schritten durch. | |||
| Wir suchen im 1. Schritt ähnliche Dreiecke. | 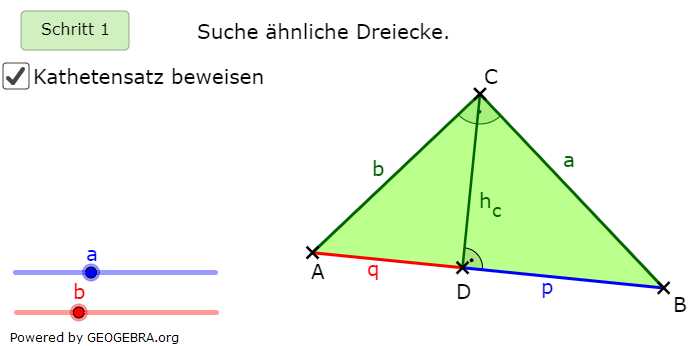 |
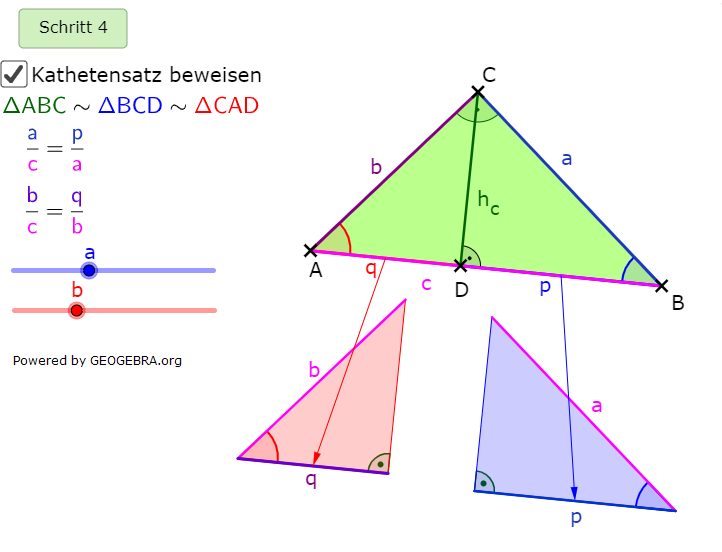
| Im 2. Schritt stellen wir fest, dass die Dreiecke ΔABC, ΔBCD sowie ΔCAD ähnlich sind, denn alle drei Dreiecke haben einen rechten Winkel sowie identisch große Basiswinkel an den jeweiligen Hypotenusen. | 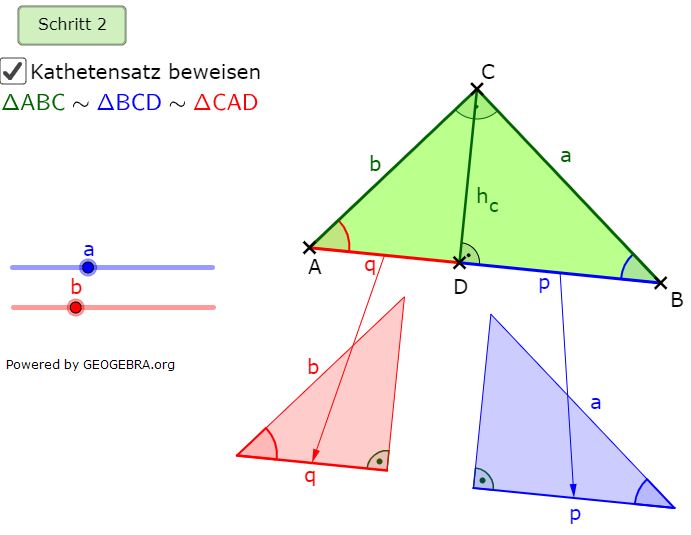 |
| Im 3. Schritt suchen wir sich entsprechende Seitenverhältnisse mit den Seiten a bzw. b. | 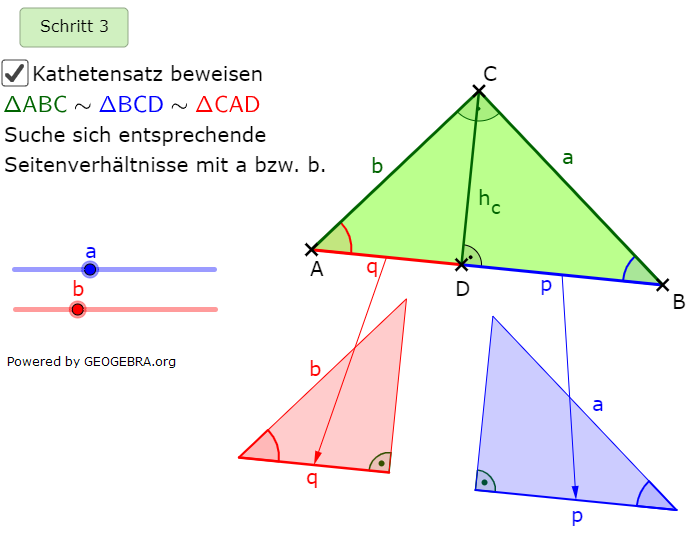 |
Wir stellen die Ähnlichkeiten von ΔABC und ΔBCD fest mit 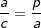 sowie für ΔABC und ΔCAD mit sowie für ΔABC und ΔCAD mit 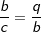 . . |
 |
| Durch Gleichungsumstellung der Ähnlichkeitsverhältnisse aus Schritt 4 erhalten wir letztendlich den Beweis des Kathetensatzes, nämlich: | 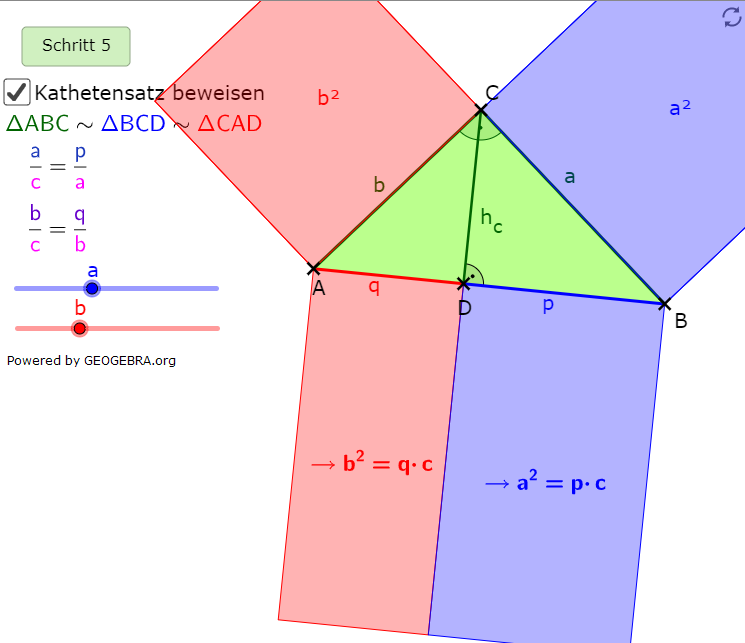 |
|||
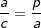 |
| | ⋅ a | ||
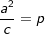 |
| | ⋅ c | ||
| a2=p∙c | ||||
| sowie | ||||
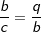 |
| | ⋅ b | ||
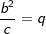 |
| | ⋅ c | ||
| b2=q∙c | ||||
|
||||
Beweisführung anders
| Eine mögliche zweite Beweisart führt uns zum Satz des Pythagoras und dem Höhensatz des Euklid. Im neben abgebildeten rechtwinkligen Dreieck gilt: |
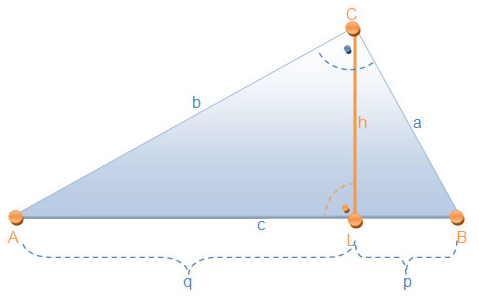 |
|||
| b2=q2+h2 | Satz des Pythagoras | |||
| h2=p⋅q | Höhensatz des Euklid | |||
| b2=q2+p⋅q | ||||
| b2=q(q+p) | (q ausgeklammert) | |||
| Wegen q+p=c gilt damit: | ||||
| b2=q⋅c | ||||
Identische Vorgehensweise für |
||||
| a2=p2+h2 | Satz des Pythagoras | |||
| h2=p⋅q | Höhensatz des Euklid | |||
| a2=p2+p⋅q | ||||
| a2=p(p+q) | (p ausgeklammert) | |||
| Wegen p+q=c gilt damit: | ||||
| a2=p⋅c | ||||
|
||||
| Du befindest dich hier: |
| Ähnlichkeitsbeweis Kathetensatz des Euklid |



- Geschrieben von Dr.-Ing. Meinolf Müller Dr.-Ing. Meinolf Müller
- Zuletzt aktualisiert: 06. Juli 2021 06. Juli 2021



