 |
WIKI unbestimmtes Integral - Integrationsregeln Basis |

| Titel Aufgabenblatt | Level / Blattnr. |
| Integral und Stammfunktion Basisaufgaben Aufgabenbl. Level 1 / Blatt 1 21 Aufgaben im Blatt |
| Integral und Stammfunktion Basisaufgaben Aufgabenbl. Level 1 / Blatt 2 21 Aufgaben im Blatt |
| Integral und Stammfunktion Basisaufgaben Aufgabenbl. Level 1 / Blatt 3 21 Aufgaben im Blatt |
| Integral und Stammfunktion Basisaufgaben Aufgabenbl. Level 2/ Blatt 1 21 Aufgaben im Blatt |
| Integral und Stammfunktion Basisaufgaben Aufgabenbl. Level 2/ Blatt 2 13 Aufgaben im Blatt |
| Integral und Stammfunktion Trigonometrie Aufgabenbl. Level 2/ Blatt 3 25 Aufgaben im Blatt |
| Du befindest dich hier: |
| WIKI unbestimmtes Integral - Integrationsregeln Basis |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 25. Januar 2022 25. Januar 2022



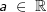 zum Faktor der Stammfunktion wird.
zum Faktor der Stammfunktion wird.
 mit
mit  und zusätzlich
und zusätzlich 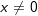 falls n<-1.
falls n<-1. .
. .
. .
. .
. .
. .
. .
. und x>0 gilt:
und x>0 gilt:
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.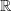 differenzierbare Funktion. Dann gilt:
differenzierbare Funktion. Dann gilt: .
.


 . Wir substitieren z=u(x) dann ist
. Wir substitieren z=u(x) dann ist  . Nun bilden wir
. Nun bilden wir  . Diesen Ausdruck stellen wir um nach dx:
. Diesen Ausdruck stellen wir um nach dx:  . Jetzt ersetzen wir dx im Integral durch diesen Ausruck und erhalten
. Jetzt ersetzen wir dx im Integral durch diesen Ausruck und erhalten 
 .
. .
. .
.

 .
. .
. , die innere Funktion ist
, die innere Funktion ist  .
. . Die
. Die  .
.
























