| Luke lebt auf dem Wüstenplaneten Tatooine mit den Koordinaten T(2|6|5). Er möchte in vier Stunden mit seinem Sternenjäger auf dem Planeten Naboo am Punkt N(6|-2|1) eintreffen, um dort seine Schwester Leia wieder zu sehen. Gemeinsam wollen sie versuchen, den Krieg der Sterne zu verhindern. |
 |
| a) |
Berechne den Abstand der beiden Planeten in Sternkilometern. |
| b) |
Stelle eine Parametergleichung für die Flugbahn von Luke auf. Beachte dabei, dass der Parameter t die vergangene Zeit in Stunden angeben soll. |
| c) |
Genau in der Mitte der Flugstrecke an der Position M sendet Luke eine Nachricht an Leia, dass er pünktlich ankommen wird. Die Nachricht wird mit einer Geschwindigkeit übertragen, die viermal so groß ist, wie seine Fluggeschwindigkeit.
Stelle eine Parametergleichung für die Nachricht auf (Parameter s=0 bei M). Beschreibe, woran man erkennt, dass beide Parametergleichungen dieselbe Gerade beschreiben. Berechne die Sternzeit, an der die Nachricht ankommt. |
| Das Imperium hat den Weltraum mit den Koordinatenebenen in acht Teile eingeteilt. Die Koordinatenebenen werden mit Sonden überwacht. |
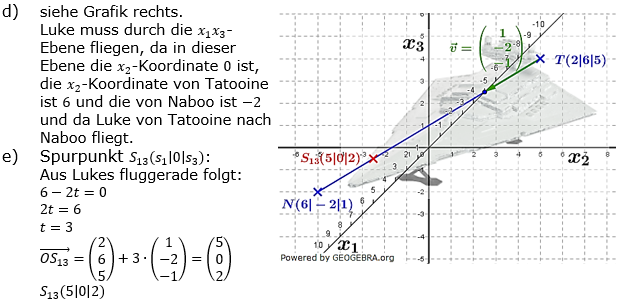
| d) |
Zeichne in ein geeignetes Koordinatensystem alle Punkte und die Flugbahn von Luke ein. Begründe, warum Luke durch die x1x3-Ebene fliegen muss. |
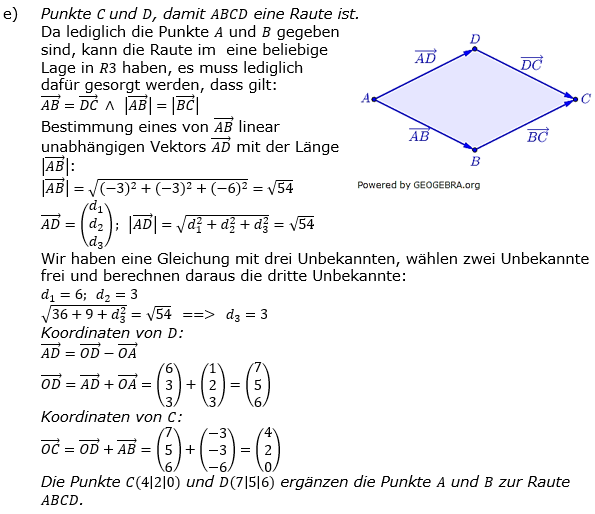
| e) |
An dem „Durchflugpunkt“ durch die x1x3-Ebene befindet sich eine Sonde des Imperiums. Berechne diesen Spurpunkt S13 und zeichne ihn ein. |
| f) |
Die Sonde sendet beim Vorbeiflug von Luke eine Nachricht an den Sternenkreuzer von Darth Vader im Punkt D(0|0|5). Die Nachricht kommt nach eine halben Stunde an. Zu diesem Zeitpunkt (Parameter r=0) schickt Darth Vader einen Droiden-Sternjäger in Richtung des Vektors 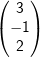 los. los.
Zeige, dass Naboo auf der Flugbahn des Droiden-Sternjägers liegt.
Berechne, welcher der beiden Sternjäger schneller fliegt.
Überprüfe, ob Luke und Leia genügend Zeit für eine Flucht bleibt, indem du die Sternzeit berechnest, an der der Droiden-Sternjäger auf Naboo ankommt. |

 .
.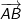 .
.
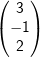 los.
los.