|
Analytische Geometrie | Vektorgeometrie – Training - Aufgabenblatt 02 |
| Dokument mit 10 Aufgaben |
Aufgabe A1
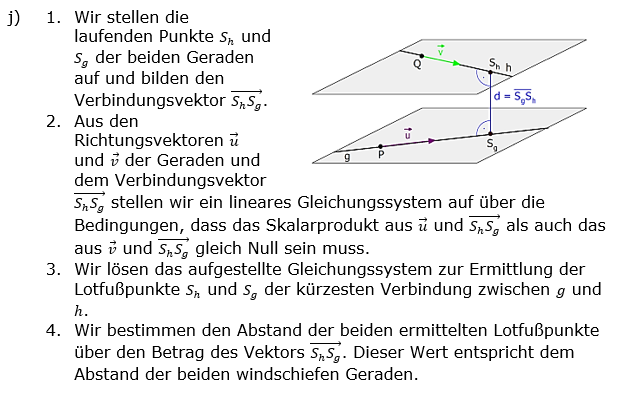
| Das Saarpolygon | |
Abbildung 1 Das Saarpolygon">Von Markscheider - Eigenes Werk, CC BY-SA 4.0 |
Abbildung 2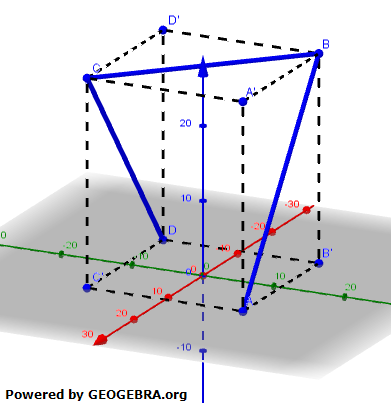 |
Die Abbildung 1 zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken 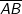 , , 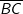 und und 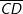 mit A(11|11|0), B(-11|11|28), C(11|-11|28) und A(-11|-11|0) besteht (vgl. Abbildung 2). mit A(11|11|0), B(-11|11|28), C(11|-11|28) und A(-11|-11|0) besteht (vgl. Abbildung 2). |
|
| A, B, C und D sind die Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. | |
| a) | Begründe, dass die Punkte B und C symmetrisch bezüglich der x3-Achse liegen. |
| b) | Berechne die Länge des Streckenzuges in Wirklichkeit. |
Im Punkt S(1|2|6) wird von einer Firma ein Scheinwerfer installiert, der die Strecke 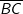 des Saarpolygons von unten anstrahlt. Die Firma behauptet, dass der Scheinwerfer 22 m von der Strecke des Saarpolygons von unten anstrahlt. Die Firma behauptet, dass der Scheinwerfer 22 m von der Strecke 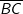 entfernt aufgestellt wurde. entfernt aufgestellt wurde. |
|
| c) | Beurteile die Aussage der Firma durch geeignete Rechnungen. |
| Die Ebene E enthält die Punkte A, B und C, die Ebene F die Punkte B, C und D. | |
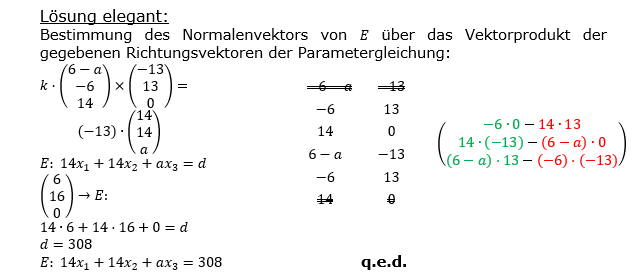
| d) | Bestimme eine Gleichung von E in Koordinatenform. |
| (Zur Kontrolle: 14x1+14x2+11x3=308) | |
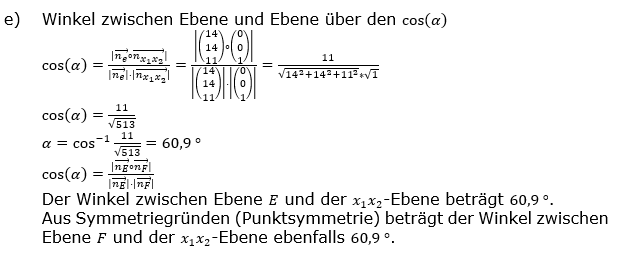
| e) | Berechne die Größe α des Winkels, unter dem die Ebene E die x1x2-Ebene schneidet. Gib einen Term an, mit dem man aus α die Größe des Winkels zwischen den Ebenen E und F berechnen kann. |
| f) | Die Ebene E ist Teil einer Ebenenschar Ea: 14x1+14x2+ax3=308; a ∈ R. Begründe, dass der Punkt P(14|8|0) zu allen Ebenen der Schar gehört und weise nach, dass die Ebenenschar auch durch die Parametergleichung |
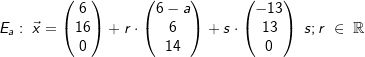 beschrieben werden kann. beschrieben werden kann. |
|
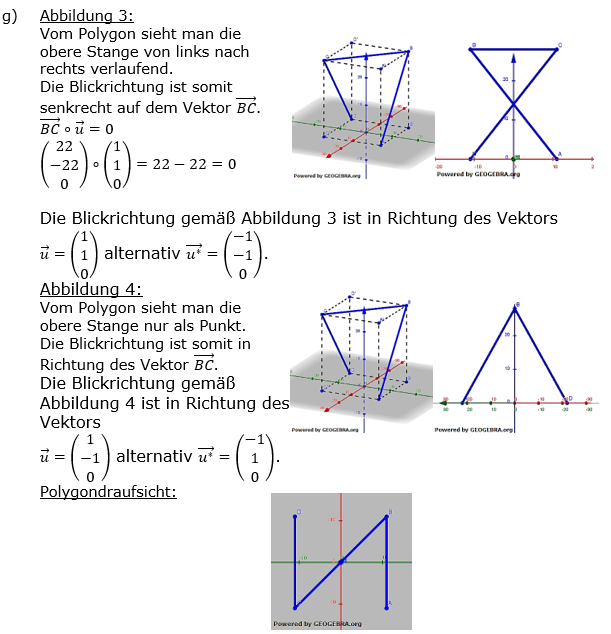
| g) | Das Saarpolygon wird aus verschiedenen Blickrichtungen betrachtet. Die Abbildungen 3 und 4 stellen das Saarpolygon für zwei Blickrichtungen schematisch dar. Gib zu jeder der beiden Abbildungen 3 und 4 einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibt. Stelle das Saarpolygon schematisch für eine Betrachtung von oben dar. |
Abbildung 3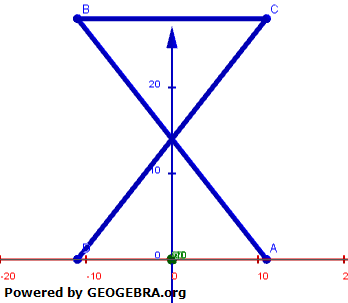 |
Abbildung 4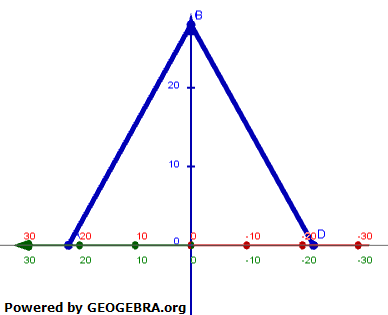 |
|
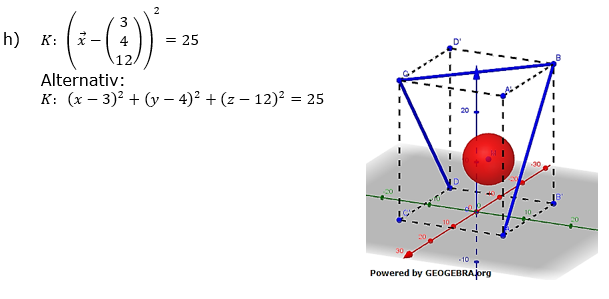
| Der Punkt M(3|4|12) ist Mittelpunkt eines kugelförmigen Luftballons mit einem Durchmesser von 5 m, der zur Dekoration autgehangen wird. | ||
| h) | Gib die entsprechende Kugelgleichung zum Luftballon an. | |
| i) | Der kugelförmige Luftballon ist Teil einer Kugelschar mit den Mittelpunkten Ma(3a|4a|12a) a ∈ R. Begründe, dass alle Mittelpunkte auf einer Geraden liegen. | |
| j) | Die Gerade aus Teilaufgabe i) und die Gerade, welche die Strecke 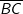 enthält, haben keinen Schnittpunkt. Erläutere unter Nutzung von Fachbegriffen (und OHNE konkrete Rechnungen) ein Vorgehen, um den Abstand dieser beiden Geraden zu ermitteln. enthält, haben keinen Schnittpunkt. Erläutere unter Nutzung von Fachbegriffen (und OHNE konkrete Rechnungen) ein Vorgehen, um den Abstand dieser beiden Geraden zu ermitteln. |
|
| |
| Du befindest dich hier: |
| Analytische Geometrie | Vektorgeometrie – Training - Aufgabenblatt 02 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 01. Januar 2023 01. Januar 2023