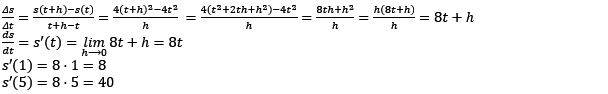|
Vom Differenzenquotienten zur Ableitung - Level 3 - Expert - Blatt 1 |
| Dokument mit 10 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
Ein Fahrzeug wird abgebremst. Für den in der Zeit t (in Sekunden) zurückgelegten Weg s(t) (in Metern) gilt: s(t)=20t-t2; t∈[0;10].
|
| |
Aufgabe A2
| Ein Körper bewegt sich so, dass er in der Zeit t den Weg s(t)=4t2 (s in m, t in s) zurücklegt. Bestimme mithilfe des Differenzenquotienten die momentane Änderungsrate von s(t) zu den Zeiten t0=1 und t1=5. Welche Bedeutung hat die momentane Änderungsrate von s(t)? |
| |
Aufgabe A3 (4 Teilaufgaben)
Begründe (ohne zu rechnen), welches Vorzeichen die Ableitung der Funktion f mit f(x)=-x3+5 an der Stelle x0 hat.
|
| |
Aufgabe A4 (2 Teilaufgaben)
Die Funktion f mit f(x)=-0,0075x2+3x beschreibt modellhaft die Baukosten für eine Wohnung von x m2 Wohnfläche (20 ≤ x ≤ 200, f(x) in 1000 €). Es ist f' (x)=-0,015x+3.
|
| |
| Du befindest dich hier: |
| Vom Differenzenquotienten zur Ableitung - Level 3 - Expert - Blatt 1 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 23. November 2021 23. November 2021

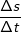 die momentane Änderungsrate s'(t) des Fahrzeugs nach 6 und nach 10 Sekunden.
die momentane Änderungsrate s'(t) des Fahrzeugs nach 6 und nach 10 Sekunden.