| Detaillierte Lösung für a) |
|
In diesem Beispiel ist die äußere Funktion eine Potenzfunktion, erkenntlich an )4. Also leitest du erst einmal ganz einfach nach der Potenzregel ab und schreibst f'(x)=4(5-3x)3.
Jetzt kommt wegen der Kettenregel die innere Funktion dran, das ist der Ausdruck in der Klammer mit 5-3x. Dieser Ausdruck abgeleitet ergibt -3. Nun musst du die abgeleitete Potenzfunktion nur noch mit der Ableitung -3 der inneren Funktion multiplizieren und hast das endgültige Ergebnis:
f'(x)=4(5-3x)3⋅(-3)=-12(5-3x)3. |
| b) |
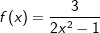
In diesem Beispiel ist die 3 ein Faktor, der nach der Faktorregel erhalten bleibt.
Der Ausdruck (2x2-1)-1 ist die Verkettung einer Potenzfunktion als äußerer Funktion mit einer quadratischen Funktion als innere Funktion. Gemäß Kettenregel gilt:
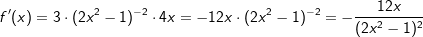 |
| c) |
f(x)=3sin(3x2)
In diesem Beispiel ist die äußere und innere 3 ein Faktor, der nach der Faktorregel erhalten bleibt.
Der Ausdruck sin(3x2) ist die Verkettung einer Sinusfunktion als äußerer Funktion mit einer quadratischen Funktion als innerer Funktion. Gemäß der Kettenregel gilt:
f'(x)=3⋅cos(3x2)⋅2⋅3x=18x⋅cos(3x2). |
|
Hinweis: |
Bei den trigonometrischen Funktionen sin, cos und tan ändert sich beim Ableiten das Argument der Funktion (das Argument ist der Ausdruck, der bei sin, cos und tan in der Klammer steht) NIE !!!
Bei Exponentialfunktionen (z. B. f(x)=a3x-2) ändert sich beim Ableiten der Exponent NIE !!! |




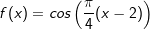 ist eine verkettete Funktion mit u(x)=cos(x) und
ist eine verkettete Funktion mit u(x)=cos(x) und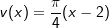 .
.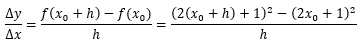
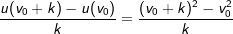 bzw.
bzw.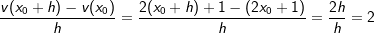
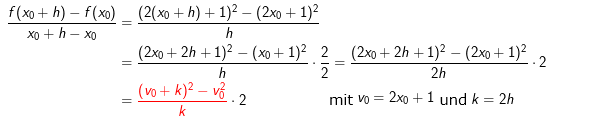
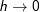 auch
auch 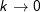 und wir erhalten:
und wir erhalten: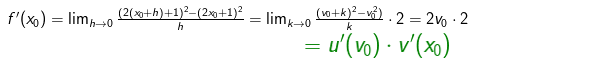
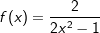
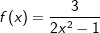
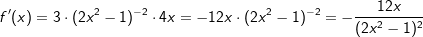









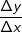 für Δx⟶0.
für Δx⟶0.