 |
|
Tangente und Normale der Differenzialrechnung |


Tangente und Normale - Einleitung
| Nachdem wir nun alle Ableitungsregeln kennen, stellt sich doch die Frage, was wir damit anfangen können. Eines dieser Anwendungsgebiete beschäftigt sich mit der Aufstellung von Tangenten- bzw. Normalengleichungen in bestimmten Punkten von Graphen anderer Funktionen bzw. legen von Tangenten von bestimmten Punkten aus an den Graphen einer Funktion. |
Tangente und Normale in bestimmten Punkten
Tangentengleichung über die Geradengleichung
 Wegen Reparaturarbeiten ist der Austausch von acht Seitenträgern des Eiffelturms erforderlich. Die Seitenträger beginnen in einem Punkt des unteren Bogens und enden kurz vor dem ersten Aussichtsplateau des Turms. Wegen Reparaturarbeiten ist der Austausch von acht Seitenträgern des Eiffelturms erforderlich. Die Seitenträger beginnen in einem Punkt des unteren Bogens und enden kurz vor dem ersten Aussichtsplateau des Turms.Für die Anfertigung der neuen Träger wird eine Konstruktionszeichnung benötigt, um die Arbeiten in Auftrag geben zu können. Hierzu muss zunächst die Schrägstellung sowie die Länge des Trägers ermittelt werden. Eine Architektengruppe fertigte Bilder der Situation im geeigneten Maßstab an. Die obige Grafik zeigt die Situation, einer der acht auszutauschenden Träger ist in der Grafik rot gekennzeichnet. Die Aufnahmen wurden digitalisiert und vermessen. Dabei wurde festgestellt, dass der Bogen durch f(x)=-0,00096x4+0,0002x3-0,05537x2-0,002x+6 beschrieben werden kann. Der Ansatzpunkt des schrägen Trägers am Bogen liegt im Punkt P(-5,8|3,0). Der Träger geht in diesem Punkt tangential in den Bogen über. Gesucht wird die Funktionsgleichung g, die den Verlauf des Trägers beschreibt. Eine solche, wie auch immer geartete Aufgabenstellung ist ein Tangentenproblem in einem bestimmten Punkt des Graphen einer Funktion. In unserem Beispiel stellt die Funktion f den Verlauf des Bogens dar, der Punkt P liegt auf dem Bogen, wird also durch die Funktionsgleichung von f beschrieben und der Träger wird zur Tangente an den Bogen im Punkt P. Hieraus ergeben sich die nachfolgenden Bedingungen: Soll der Träger im Punkt P den Bogen tangential berühren, so muss die Geradengleichung des Trägers dieselbe Steigung haben, wie der Bogen selbst im Punkt P. Zudem liegt P außer auf dem Bogen selbst auch auf der Tangente. Also beschreibt auch die Tangentengleichung den Punkt P ebenso. Eine Tangente ist mathematisch gesehen eine Grade mit der Funktionsgleichung y=mx+c, wobei m die Steigung der Geraden und c deren Schnittpunkt mit der y-Achse ist (y-Achsenabschnitt). Somit benötigen wir zunächst die Steigung m. Da diese gleich groß sein muss wie die Steigung des Bogens im Punkt P, können wir diese über die erste Ableitung der Funktionsgleichung des Bogens berechnen. f(x)=-0,00096x4+0,00002x3-0,05537x2-0,0023x+6 f'(x)=-0,00384x3+0,00006x2-0,11047x-0,0023 Der Punkt P hat die x-Koordinate -5,8, also benötigen wir f'(-5,8). f'(-5,8)=-0,00384⋅(-5,8)3+0,00006⋅(-5,8)2-0,11047⋅(-5,8)-0,0023=1,39 Die Tangente hat etwa die Steigung m=1,39, die Tangentengleichung ist somit zunächst y=1,39x+c. Jetzt benötigen wir noch den Wert von c. Da aber P auf der Tangente liegt, können wir den Punkt P in die Tangentengleichung einsetzen und daraus c berechnen. 3,0=1,39⋅(-5,8)+c 3,0=-8,004+c | +8,004 c=11,004 Die Geradengleichung, die den Verlauf des Trägers beschreibt, lautet somit: y=1,39x+11,004 |
Tangentengleichung über die Punkt-Steigungs-Formel
| Die zuvor beschriebene Aufstellung der Geradengleichung der Tangente entspricht der Vorgehensweise zum Aufstellen von Geraden in Klasse 8 bzw. Klasse 9. Wegen der etwas umständlichen Berechnung lernen wir hier nun eine elegantere Methode kennen, ohne die wir Aufgaben eines späteren Kapitels auch nicht lösen können. Zunächst beschreiben wir die Tangentengleichung nicht mehr mit der Variablen y, sondern vielmehr beginnen wir mit t(x). Das t steht hier für Tangente, mit t(x) weiß jeder, dass nachfolgend eine Tangentengleichung beschrieben wird. Dann merken wir uns die Punkt-Steigungs-Formel einer Geraden. Für diese gilt: Ist ein Punkt P(u|f(u)) Element einer Funktion f, so lautet die Funktionsgleichung der Tangente im Punkt P: t(x)=f'(u)⋅(x-u)+f(u) Wie wir sehen, benötigen war also lediglich den Wert der Steigung des Graphen der Funktion f im Punkt P, also f'(u) und schon können wir die Tangentengleichung ohne weitere Berechnung aufstellen. Für unser obiges Beispiel bedeutet dies: f'(u)=f'(-5,8), u=-5,8 und f(u)=f(-5,8)=3. Die Gleichung des Trägers damit t(x)=1,39⋅(x+5,8)+3 (Ausmultipliziert ergibt dies wie oben t(x)=1,39x+11,004). |
Normalengleichung über die Punkt-Steigungs-Formel
 Zunächst definieren wir, was eine Normale ist. Eine Normale ist ebenfalls eine Gerade, die auf irgendeiner Tangente senkrecht (orthogonal) steht. Die Tangente ist in nebenstehender Grafik rot, die Normale grün gekennzeichnet. Zunächst definieren wir, was eine Normale ist. Eine Normale ist ebenfalls eine Gerade, die auf irgendeiner Tangente senkrecht (orthogonal) steht. Die Tangente ist in nebenstehender Grafik rot, die Normale grün gekennzeichnet.Mithilfe der Punktsteigungs-Formel ist es nun ein leichtes, die Funktionsgleichung dieser Normalen aufzustellen. Wir bezeichnen die Normale zunächst mit n(x), dann lautet die Funktionsgleichung:  Wie wir sehen, ist der einzige Unterschied zur Tangentengleichung der Ausdruck f'(u) und  . Alles andere ist identisch. Die Normalen-gleichung unseres Beispiels lautet also . Alles andere ist identisch. Die Normalen-gleichung unseres Beispiels lautet also |
Normale bei waagrechter Tangente
 Einen Sonderall stellen waagrechte Tangeten und deren zughörige Normalen dar. Waagrechte Tangenten verlaufen parallel zur x-Achse während deren Normalen parallel zur y-Achse verlaufen. Dies führt zu einer Soderform der Tangenten- bzw. Normalengleichung. Einen Sonderall stellen waagrechte Tangeten und deren zughörige Normalen dar. Waagrechte Tangenten verlaufen parallel zur x-Achse während deren Normalen parallel zur y-Achse verlaufen. Dies führt zu einer Soderform der Tangenten- bzw. Normalengleichung.Bei einer waagrechten Tangente, deren Steigung (f'(u)) ja Null ist, erhalten wir über die Punkt-Steigungs-Formel: t(x)=f(u). Da die Normale eine unendlich große Steigung hat, kann deren Gleichung nicht mehr über die Punkt-Steigungs-Formel dargestellt werden. In diesem Falle lautet ihre Gleichung x=u. |
Merksatz Tangente und Normale
| Ist P(u|f(u)) ∈ f(x), dann lautet die Gleichung der Tangenter in P(u|f(u)): | ||
| t(x)=f'(u)⋅(x-u)+f(u) | ||
| und die Gleichung der Normalen in diesem Punkt | ||
 . . |
||
| Hat f in P(u|f(u)) eine waagrechte Tangente, so lautet deren Gleichung t(x)=f(u) und die Gleichung der Normalen in diesem Punkt x=u. |
Tangente von einem bestimmten Punkt an eine Funktion
Beispiele
Beispiel 3
| Bestimme die Funktionsgleichung der Tangente an den Graphen der Funktion f mit f(x)=x⋅(x2-x-4) deren Normale parallel zur Geraden mit y=-x verläuft. |
| Die Normale muss wegen der Angabe "parallel zu y=-x" die Steigung m=-1 haben. Damit muss die Tangente wegen m1⋅m2=-1 die Steigung m=1 haben. Da somit dieselben Bedingungen herrschen wie in Beispiel 2, ist die Lösung dieser Aufgaben dieselbe, nämlich: |
 ; ; |
t2(x)=1⋅(x+1)+2=x+3 |
| (siehe auch Beispiel 2) |
Beispiel 4
| Bestimme die Funktionsgleichung der Tangente an den Graphen der Funktion f mit f(x)=x⋅(-x2+x+4) die senkrecht auf der Geraden durch die Punkte P(3|9) und Q(-1|1) steht. Berechne auch die Schnittpunkte mit den Koordinatenachsen. |
Bestimmung der Steigung der Geraden durch P und Q über 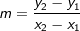 : : Bestimmung der Steigung der Tangente über mn⋅mt=-1: 2⋅mt=-1 ⇒  Bestimmung der Tangentengleichung über t(x)=f'(u)⋅(x-u)+f(u):        | p/q-Formel | p/q-Formel Auch hier erhalten wir wieder zwei Lösungen, benötigen allerdings noch f(u1) und f(u2). f(u1)=1,6⋅(-1,62+1,6+4)≈4,9 f(u2)=-0,94⋅(-(-0,942)-0,94+4)=-2   Schnittpunkte mit den Koordinatenachsen: Schnittpunkt mit der x-Achse mit t(x)=0:   N1(11,4|0) N2(-4,94|0) Schnittpunkt mit der y-Achse mit t(0):   |
Beispiel 5
Gegeben ist eine Funktion f durch  . Ihr Schaubild sei K. . Ihr Schaubild sei K.K stellt für -6≤x≤6 den Querschnitt eines 500 m langen Kanals dar (x in Meter, f(x) in Meter). Die sich anschließende Landfläche liegt auf der Höhe y=0. Der Pegelstand wird in Bezug auf den tiefsten Punkt des Kanals gemessen und beträgt maximal 2,25 m. An Land steht eine Person. In welcher Entfernung vom Kanalrand darf sie höchstens stehen, damit sie bei leerem Kanal die tiefste Stelle des Kanals sehen kann (Augenhöhe 1,50 m)? (Quelle: Abitur BW Analysis 2004). |
Dies ist eine Aufgabe zur Tangentenbildung von einem Punkt an eine Kurve. Die nebenstehende Grafik verdeutlicht die Situation. Die Sichtlinie des Beobachters ist eine Tangente an f durch die Kanalsohle. Steht er weiter weg vom Kanal als die x–Koordinate seines Beobachtungspunktes, kann er den Grund des Kanals nicht mehr sehen. Die nebenstehende Grafik verdeutlicht die Situation. Die Sichtlinie des Beobachters ist eine Tangente an f durch die Kanalsohle. Steht er weiter weg vom Kanal als die x–Koordinate seines Beobachtungspunktes, kann er den Grund des Kanals nicht mehr sehen.Die x–Koordinate seines Beobachtungspunktes ergibt sich über den Schnittpunkt der Tangente mit der Geraden y=1,5 (Augenhöhe des Beobachters). Der Berührpunkt ist P(u|f(u)), damit können wir die Punkt-Steigungsformel der Tangente aufstellen mit t(x)=f'(u)⋅(x-u)+f(u):    Die Talsohle mit T(0|-2,25) ist Punkt dieser Tangentengleichung. Wir machen eine Punktprobe mit T und erhalten:    -104u2+(u2-36)(u2+16)+2,25(u2+16)2=0 -104u2+u4-20u2-576+2,25u4+72u2+576=0 3,25u4-52u2=0 u2(3,25u2-52)=0 u1,2=0; u3=-4; u4=+4 Wir erhalten also 3 Stellen, in denen Tangenten an die Kurve gelegt werden können, die gleichzeitig durch den Punkt T(0|-2,25) verlaufen. Dies ist aus obiger Grafik auch erkennbar, in der Talsohle bei u1,2=0 haben wir eine waagrechte Tangente, bei u4=4 die Tangente zum rechten Ufer hin und wegen der Symmetrie der Funktion zum linken Ufer hin (nicht eingezeichnet) bei u3=-4. Zur Lösung der Aufgabe (Entfernung des Beobachters vom Ufer) benötigen wir die Tangente an der Stelle u4=4.  Die Tangente schneidet die Parallele zur x-Achse in Höhe der Augen des Beobachters. Schnittpunktbestimmung durch Gleichsetzung. t(x) ∩ 1,5 0,40625x-2,25=1,5 ⇒ x ≈ 9,23 Dies ist die Entfernung des Beobachters von der Symmetrieachse (y-Achse), seine Entfernung vom rechten Ufer ergibt sich unter Abzug der rechten Nullstelle der Funktion. f(x)=0 ⇒ x1,2=±6 9,23-6=3,23 Der Beobachter darf nicht mehr als 3,23 m vom rechten Uferrand entfernt sein, um bei leerem Kanal die Kanalsohle noch sehen zu können. |
| Titel Aufgabenblatt | Level / Blattnr. |
Tangente und Normale Aufgabenblatt Level 1 / Blatt 1  19 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 1/ Blatt 2  22 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 1/ Blatt 3  17 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 1/ Blatt 4  11 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 2 / Blatt 1  16 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 2 / Blatt 2  14 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 2 / Blatt 3  11 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 3 / Blatt 1  13 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 3 / Blatt 2  16 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 3 / Blatt 3  9 Aufgaben im Blatt |
Tangente und Normale Aufgabenblatt Level 3 / Blatt 4  9 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

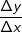 für Δx⟶0.
für Δx⟶0. Wollten wir im bisherigen Verlauf wissen, wie die Steigung einer Tangente in einem bekannten Punkt der Kurve lautet, so betrachten wir uns nun den Fall, wie die Funktionsgleichung einer Tangente lautet, die von einem Punkt, der nicht auf der Kurve liegt, an eine Kurve lautet.
Wollten wir im bisherigen Verlauf wissen, wie die Steigung einer Tangente in einem bekannten Punkt der Kurve lautet, so betrachten wir uns nun den Fall, wie die Funktionsgleichung einer Tangente lautet, die von einem Punkt, der nicht auf der Kurve liegt, an eine Kurve lautet. | p/q-Formel
| p/q-Formel Wir erhalten also zwei Werte für u, was bedeutet, dass es zwei Tangenten vom Punkt P(2,5|0) aus an den Graphen der Funktion f gibt. Mit der Kenntnis der Werte u1 und u2 können wir jetzt problemlos die beiden Tangentengleichungen aufstellen, nämlich
Wir erhalten also zwei Werte für u, was bedeutet, dass es zwei Tangenten vom Punkt P(2,5|0) aus an den Graphen der Funktion f gibt. Mit der Kenntnis der Werte u1 und u2 können wir jetzt problemlos die beiden Tangentengleichungen aufstellen, nämlich




 ;
;

