Nun gibt es ja auch Potenzfunktionen mit negativen Hochzahlen und sogar mit rationalen Hochzahlen. Betrachten wir uns zunächst einmal solche mit negativen Hochzahlen.
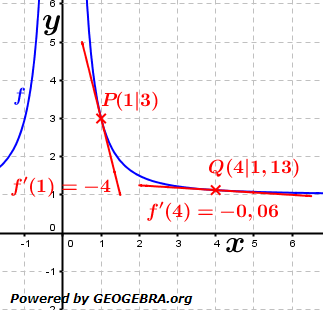 Gegeben ist die Funktion f mit Gegeben ist die Funktion f mit 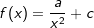 . .
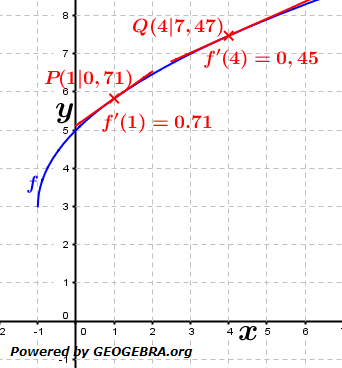
In nebenstehender Grafik haben wir für a den Wert 2 und für c den Wert 1 gewählt. Die Funktionsgleichung lautet somit 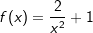 . Nach den Potenzregeln können wir auch schreiben f(x)=2 ⋅ x-2+1. . Nach den Potenzregeln können wir auch schreiben f(x)=2 ⋅ x-2+1.
Differenzenquotient:
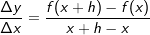
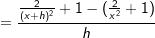
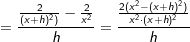
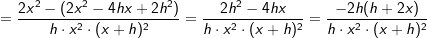
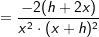
Differenzialquotient:
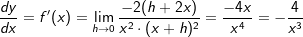
Die Ableitung der Funktion f mit 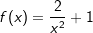 ist ist 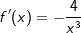 . .
Wie kommen wir nun aber mit der Potenzregel zu dieser Lösung?
Wir haben ja 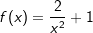 mit Hilfe der Potenzregeln umgeformt zu f(x)=2 ⋅ x-2+1. Nun können wir problemlos die Potenzregel anwenden, wir multiplizieren den Term 2⋅x-2 mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also 4x-1. Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl und erhalten mit Hilfe der Potenzregeln umgeformt zu f(x)=2 ⋅ x-2+1. Nun können wir problemlos die Potenzregel anwenden, wir multiplizieren den Term 2⋅x-2 mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also 4x-1. Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl und erhalten 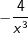 , denselben Ausdruck, den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 1 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. Somit lautet die Ableitung von , denselben Ausdruck, den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 1 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. Somit lautet die Ableitung von 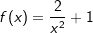
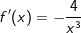 . .
Neben negativen Hochzahlen haben Potenzfunktionen auch rationale Potenzen.
 Gegeben ist die Funktion f mit Gegeben ist die Funktion f mit
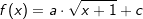 . .
In nebenstehender Abbildung haben wir für a den Wert 2 und für c den Wert 3 gewählt. Die Funktionsgleichung lautet somit:
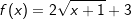 . Nach den Potenzregeln können wir auch schreiben: . Nach den Potenzregeln können wir auch schreiben:
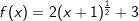 . .
Differenzenquotient:
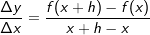
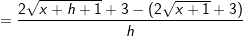
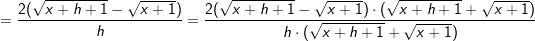
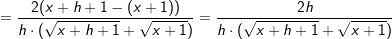
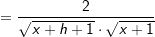
Differenzialquotient:
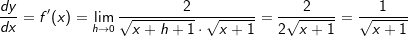
Die Ableitung der Funktion f mit 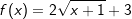 ist ist 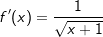 . .
Wie kommen wir nun aber mit der Potenzregel zu dieser Lösung?
Wir haben ja 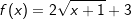 mithilfe der Potenzregeln umgeformt zu mithilfe der Potenzregeln umgeformt zu
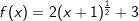 . Nun können wir problemlos die Potenzregel anwenden, wir multiplizieren den Term . Nun können wir problemlos die Potenzregel anwenden, wir multiplizieren den Term 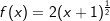 mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also 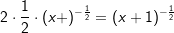 . Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl, erhalten . Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl, erhalten 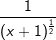 , und formen den Exponenten , und formen den Exponenten  weiter um nach den Potenzregeln, und erhalten den Ausdruck weiter um nach den Potenzregeln, und erhalten den Ausdruck 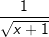 , den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 3 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. , den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 3 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen.
Somit lautet die Ableitung von 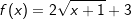
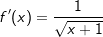 . . |




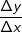 für Δx⟶0.
für Δx⟶0.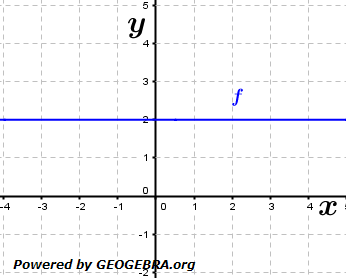 Gegeben ist die Funktion f mit f(x)=c.
Gegeben ist die Funktion f mit f(x)=c.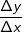 immer 0 ist, egal wie groß oder klein
immer 0 ist, egal wie groß oder klein 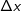 ist.
ist.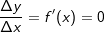 ist. Da f'(x) gleichzeitig die Steigung der Tangente im Punkt P(x|f(x)) ist, hat f(x)=2 in jedem Punkt P(x|f(x)) die Steigung 0, was ja auch aus der Abbildung ersichtlich ist.
ist. Da f'(x) gleichzeitig die Steigung der Tangente im Punkt P(x|f(x)) ist, hat f(x)=2 in jedem Punkt P(x|f(x)) die Steigung 0, was ja auch aus der Abbildung ersichtlich ist.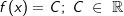 hat für alle
hat für alle 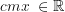 die Ableitung
die Ableitung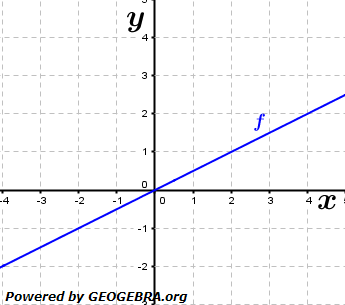 Gegeben ist die Funktion f mit f(x)=mx.
Gegeben ist die Funktion f mit f(x)=mx.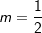 gewählt.
gewählt.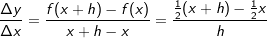
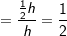
 ist, egal wie groß oder klein Δx ist.
ist, egal wie groß oder klein Δx ist.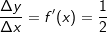 ist. Da f'(x) gleichzeitig die Steigung der Tangente im Punkt P(x|f(x)) ist, hat
ist. Da f'(x) gleichzeitig die Steigung der Tangente im Punkt P(x|f(x)) ist, hat 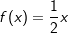 in jedem Punkt P(x|f(x)) die Steigung
in jedem Punkt P(x|f(x)) die Steigung 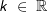 differenzierbar und es gilt:
differenzierbar und es gilt: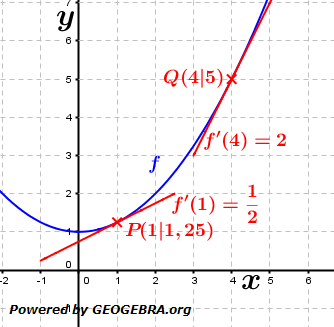 Gegeben ist die Funktion f mit f(x)=ax2+c.
Gegeben ist die Funktion f mit f(x)=ax2+c. und für c den Wert 1 gewählt. Der Graph der Funktion
und für c den Wert 1 gewählt. Der Graph der Funktion  mit
mit 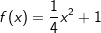 ist also eine Parabel.
ist also eine Parabel.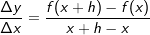
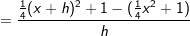
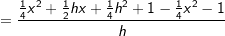
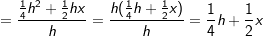
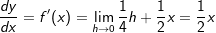
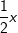 .
. 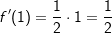 und
und 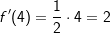 .
. bei x2 jedoch erhalten bleiben. Um aus
bei x2 jedoch erhalten bleiben. Um aus  zu machen, müssen wir
zu machen, müssen wir 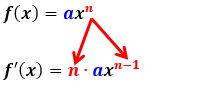 Aus der Funktionsgleichung
Aus der Funktionsgleichung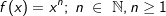 , ist differenzierbar und es gilt
, ist differenzierbar und es gilt Gegeben ist die Funktion f mit
Gegeben ist die Funktion f mit 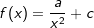 .
.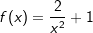 . Nach den Potenzregeln können wir auch schreiben f(x)=2 ⋅ x-2+1.
. Nach den Potenzregeln können wir auch schreiben f(x)=2 ⋅ x-2+1. 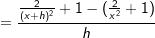
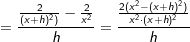
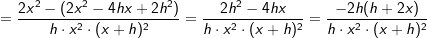
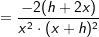
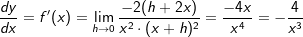
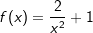 ist
ist 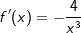 .
. 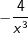 , denselben Ausdruck, den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 1 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. Somit lautet die Ableitung von
, denselben Ausdruck, den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 1 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. Somit lautet die Ableitung von 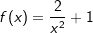
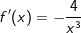 .
. Gegeben ist die Funktion f mit
Gegeben ist die Funktion f mit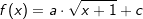 .
.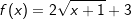 . Nach den Potenzregeln können wir auch schreiben:
. Nach den Potenzregeln können wir auch schreiben: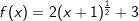 .
.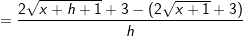
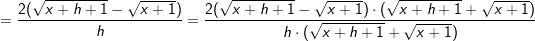
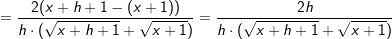
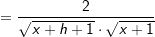
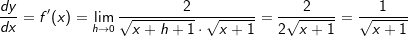
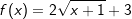 ist
ist 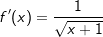 .
. 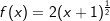 mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also
mit seinem Exponenten und vermindern dann die den Exponenten um 1, erhalten also 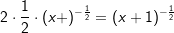 . Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl, erhalten
. Nun formen wir die negative Hochzahl nach den Potenzregeln wieder um zu einer positiven Hochzahl, erhalten 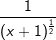 , und formen den Exponenten
, und formen den Exponenten 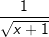 , den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 3 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen.
, den wir auch über den Differenzialquotienten erhalten haben. Das absolute Glied 3 der ursprünglichen Funktionsgleichung ist nach der Konstantenregel ja weggefallen. 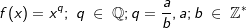 , ist differenzierbar und es gilt
, ist differenzierbar und es gilt








